Сравнение двух частотных распределений. Критерий хи-квадрат

В практике биологических исследований часто бывает необ­ходимо проверить ту или иную гипотезу, т. е. выяснить, насколь­ко полученный экспериментатором фактический материал под­тверждает теоретическое предположение, насколько анализиру­емые данные совпадают с теоретически ожидаемыми. Возника­ет задача статистической оценки разницы между фактическими данными и теоретическим ожиданием, установления того, в ка­ких случаях и с какой степенью вероятности можно считать эту разницу достоверной и, наоборот, когда ее следует считать не­существенной, незначимой, находящейся в пределах случайнос­ти. В последнем случае сохраняется гипотеза, на основе кото­рой рассчитаны теоретически ожидаемые данные или показа­тели. Таким вариационно-статистическим приемом проверки гипо­тезы служит метод хи-квадрат (χ ²). Этот показатель часто на­зывают «критерием соответствия» или «критерием согласия» Пирсона. С его помощью можно с той или иной вероятностью судить о степени соответствия эмпирически полученных данных теоретически ожидаемым.

С формальных позиций сравниваются два вариационных ряда, две совокупности: одна – эмпирическое распределение, другая представляет собой выборку с теми же параметрами (n, M, S и др.), что и эмпирическая, но ее частотное распределение построено в точном соответствии с выбранным теоретическим законом (нормальным, Пуассона, биномиальным и др.), которому предположительно подчиняется поведение изучаемой случайной величины.

В общем виде формула критерия соответствия может быть записана следующим образом:

,

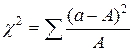где a – фактическая частота наблюдений,

A – теоретически ожидаемая частота для данного класса.

Нулевая гипотеза предполагает, что достоверных различий между сравниваемыми распределениями нет. Для оценки существенности этих различий следует обра­титься к специальной таблице критических значений хи-квад­рат (табл. 9 П) и, сравнив вычисленную величину χ ² с табличной, решить, достоверно или не достоверно отклоня­ется эмпирическое распределение от теоретического. Тем самым гипотеза об отсутствии этих различий будет либо опровергнута, либо оставлена в силе. Если вычисленная величина χ ² равна или превышает табличную χ ²_{(α, df )}, решают, что эмпирическое распределение от теоретического отличается достоверно. Тем самым гипотеза об отсутствии этих различий будет опровергнута. Если же χ ² < χ ²_{(α, df )}, нулевая гипотеза остается в силе. Обычно принято считать допустимым уро­вень значимости α = 0.05, т. к. в этом случае остается только 5% шансов, что нулевая гипотеза правильна и, следовательно, есть достаточно оснований (95%), чтобы от нее отказаться.

Определенную проблему составляет правильное определение числа степеней свободы (df), для которых из таблицы берут значения критерия. Для определения числа степеней свободы из общего числа классов k нужно вычесть число ограничений (т. е. число параметров, использованных для расчета теоретических частот).

В зависимости от типа распределения изучаемого признака формула для расчета числа степеней свободы будет меняться. Для альтернативного распределения (k = 2) в расчетах участвует только один параметр (объем выборки), следовательно, число степеней свободы составляет df = k −1=2−1=1. Для полиномиального распределения формула аналогична: df = k −1. Для проверки соответствия вариационного ряда распределению Пуассона используются уже два параметра – объем выборки и среднее значение (числен­но совпадающее с дисперсией); число степеней свободы df = k −2. При проверке соответ­ствия эмпирического распределения вариант нормальному или биномиальному закону число степеней свободы берется как число фактических классов минус три условия построения рядов – объем выборки, сред­няя и дисперсия, df = k −3. Сразу стоит отметить, что критерий χ² работает только для выборок объемом не менее 25 вариант, а частоты отдельных классов должны быть не ниже 4.

Вначале проиллюстрируем применение критерия хи-квадрат на примере анали­за альтернативной изменчивости. В одном из опытов по изуче­нию наследственности у томатов было обнаружено 3629 крас­ных и 1176 желтых плодов. Теоретическое соотношение частот при расщеплении признаков во втором гибридном поколении должно быть 3:1 (75% к 25%). Выполняется ли оно? Иными словами, взята ли данная выборка из той генеральной совокупности, в которой соотношение частот 3:1 или 0.75:0.25?

Сформируем таблицу (табл. 4), заполнив значениями эмпирических частот и результатами расчета теоретических частот по формуле:

А = n∙p,

где p – теоретические частости (доли вариант данного типа),

n – объем выборки.

Например, A ₂ = n∙p ₂ = 4805∙0.25 = 1201.25 ≈ 1201.

Таблица 4

Значение (цвет плода), xj	Фактическая частота, a	Теоретическая частость, p	Теорети­ческая частота, А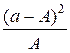
Красный		0.75		0.187621
Желтый		0.25		0.5204
Сумма	n = Σ a = 4805		n = Σ A = 4805	χ ² = 0.71

Далее вычисляем хи-квадрат χ ² = 0.71 и число степеней свободы (при двух классах и одном ограничении, объеме выборки) df = k − 1 = 2 − 1 = 1. По табл. 9 П находим критическое значение χ ²_{(0.05, 1)} = 3.84. Поскольку полученная величина (0.71) меньше табличной (3.84), различия сравниваемых распределений ста­тистически недостоверны. Иначе говоря, фактические частоты хорошо согласуются с теоретически ожидаемыми. Полученные данные не отвергают принятую ги­потезу о том, что в нашем случае имеется соотношение 3:1.

Здесь следует еще раз обратить внимание читателей на то обстоятельство, что сохранение нулевой гипотезы нельзя считать доказательством справедливости нулевой гипотезы. Результатами представленных вычислений теория о расщеплении по фенотипам в соотношении 3:1 не доказана, хотя и не опровергнута. Статистика доказывает только факт отличий, но не их отсутствие. Чтобы доказать теорию, нужно предположить анти-теорию (например, соотношение 1:1) и опровергнуть ее с помощью статистических приемов.

В процессе другого исследования добыты 671 самец и 569 са­мок. Требуется определить, подтверждают ли эти данные факт преобладания самцов или налицо просто случайное отличие цифр. Теоретическое отношение признаков (соотношение по­лов) 1:1. Подтверждается ли оно? Находим сумму 671+569=1240, среднее 620,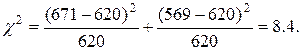

Сравнение вычисленного (8.4) и критического значения (для df = 1 и α = 0.05 χ ²_{(0.05, 1)} = 3.84) явно свидетельствует о существенном отклонении фактического соотношения полов от гипотезы – 1:1. Вероятность правильности нулевой гипотезы (т. е. что в данном случае действительно имеет место численное равенст­во полов) оказалась даже меньше 0.01. Следовательно, есть все основания говорить о достоверном преобладании самцов.

В качестве первого примера решим задачу, соответствует ли закону Пуассона распределение числа повторных отловов альбатросов (табл. 5). В этом случае рассматривается процесс, этапами которого выступают события «отлов птицы». В чреде таких событий встречаются редкие – «отлов меченной особи». Биологическая подоплека состоит в следующем: случайны ли повторные отловы птиц или есть факторы, ответственные за нарушение случайности? Например, птицы могут приманиваться и стремиться попасться вновь либо могут стараться избежать повторного отлова. В обоих случаях птицы будут «умышленно» попадаться чаще или реже, нарушая случайность повторного отлова и искажая тем самым форму распределения, которое будет отходить от формы, предписанной законом Пуассона. Согласно нулевой гипотезе, птицы ведут себя случайно, их встречаемость соответствует этому закону. Алгоритм расчетов теоретических частот для этого случая прост и основан на формулах прямого расчета теоретических частот:

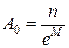(частота нулевого класса),

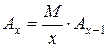(частота прочих классов),

где М – средняя арифметическая ряда,

x – значение ряда (число объектов в пробе),

A_x – теоретическая частота значения x,

n – объем выборки (число проб),

e = 2.7183…– основание натурального логарифма.

Параметры данного вариационного ряда были рассчитаны выше (с. 23): M = 0.968. Теоретическая частота нулевого значения равна:

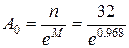= 11.93803 ≈ 12,

частота значения x = 1:

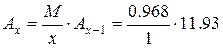= 11.55602 ≈ 11

и т. д. (табл. 5, графа 3).

Таблица 5

Число повторных отловов, x	Фактическая частота, a	Теоретическая частота, A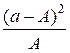
					0.75
					1.45
	7
					0.17
Сумма	n = Σ a = 32		n = Σ A = 32		χ² = 2.31

По окончании вычислений получаем два ряда частот, отли­чия между которыми оцениваются по критерию хи-квадрат.

Перед расчетом значения критерия следует убедиться, что выполнены требования к данным для расчета критерия χ ²:

– объем выборки более 25 вариант, n > 25,

– суммы эмпирических и теоретических частот равны объему выборки n = Σ a = Σ A (с точностью не ниже 1-2%),

– все классы эмпирического и теоретического рядов имеют частоты более 4, a_j > 4; если какие-либо классы имеют меньше 4 вариант (у нас значения 3 и 4 имеют частоты 2 и 1), то они должны быть объединены (суммированы) с соседними, что и показано в таблице с помощью фигурных скобок.

Далее вычисляем значения критерия: для первой строки

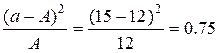
и т. д. (графа 4), итого χ ² = 2.31.

Число степеней свободы находим как число окончательных классов (3) минус число ограничений: df = k −2 = 3−2 = 1.

Табличное значение χ ²_(0.05,1) = 3.84. Полученная вели­чина (2.31) меньше табличной (3.84), следовательно, нулевая гипоте­за не отвергается: эмпирическое распределение достоверно не отличается от распределения Пуассона. Иными словами, у нас нет оснований утверждать, что вероятность повторного отлова изменяется: нельзя утверждать, что сама операция отлова привлекает или пугает птиц.

Соответствие эмпирического ряда распределению Пуассона можно проверить и другим способом: сравнив по критерию Фишера величины средней арифметической и дисперсии для числа степеней свободы df ₁ = n − 1, df ₂ = n − 1. В нашем случае M = 0.968, S ² = 1.257, F = 1.257 / 0.968 = 1.157. По­скольку эта величина меньше табличной (F _{(0.05, 31, 31)} = 1.84), сравниваемые показатели достоверно не отличаются, а равенство средней и дисперсии ха­рактерно лишь для распределения Пуассона.

При статистическом исследовании непрерывных признаков нужно быть уверенным, что они действительно подчиняются нормальному закону, а в случае дискретных признаков – биномиальному. Для такой проверки нулевая гипотеза звучит так: «получен­ное распределение соответствует нормальному (биномиальному)» или «выборка взята из генеральной совокупности, подчиняющейся закону нормального (биномиального) распределения». Все вычислительные опе­рации для случаев нормального и биномиального распределе­ний совпадают. Рассмотрим проверку первой гипотезы.

Расчеты начинаются с построения вариационного ряда и поиска центральных значений для каждого класса (табл. 6 и 7). Далее по формуле 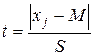вычисляются нормированные отклонения середины каждого классового интервала (x_j) от общей средней M (S – стандартное отклонение). В нашем случае M = 9.29 г, S = 0.897 г., тогда, например для второго интервала получаем: t = |8.05 − 9.27| / 0.897 = 1.38. Далее определяем теоретические частости нормального распределения, или ординаты нор­мальной кривой (табл. 4 П), соответствующие вы­численным нормированным отклонениям. Для t = 1.38 находим p = 0.1539 ≈ 0.15 (табл. 6, графа 5). (Заметим, что модуль в формуле нормированных отклонений берется потому, что в таблице 6 П приведены частости p только для положительных значений t.) Следующая операция, вычисление теоретических частот, ведется по формуле:

А = с∙p,

где p – ординаты нормальной кривой,

с – константа ряда, оп­ределяемая по формуле ,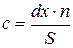

dx – классовый интервал (в дан­ном случае он равен 0.7) (см. с. 13),

п – объем выборки (63).

Для нашего примера 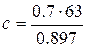= 49.16.

Таблица 6

Классовые интервалы	Центр интервала, xj	Фактическая частота, a	Нормиро­ванное от­клонение, t	Ординаты нормаль­ной кривой, p	Теоретическая частота, А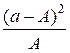
7 – 7.7	7.35	2	2.16	0.04
7.8 – 8.4	8.05		1.38	0.15
8.5 – 9.1	8.75		0.60	0.33		0.25
9.2 – 9.8	9.45		0.18	0.39		0.47
9.9 – 10.5	10.15		0.96	0.25		0.33
10.6 – 11.2	10.85		1.74	0.09
11.3 – 11.9	11.55		2.52	0.02
Σ		n= Σ a = 63			n =Σ A = 63	χ ² = 1.36

Теоретическая частота для f = 0.15 составит:

А = 49.16∙0.1539 = 7.55 ≈ 8 (графа 6).

В результате вычислений получаем теоретическое нормальное распределение с параметрами M = 9.29 г, S = 0.897 г, п = 63 (см. рис. 4, с. 20).

Перед расчетом кри­терия хи-квадрат проверяем сов­падение суммы эмпирических и теоретических частот (по 63 ва­рианты) и минимальные объемы в отдельных классах. Поскольку в крайних классах частоты были ниже 4, проводим их объединение (отмечено скобками), после чего число классов сократилось до k = 5. Вычисляем значения χ ²: для первого класса (9 − 10)² / 10 = = 0.1, для всего ряда χ ² = 1.36. Число степеней свободы df = 5 − 3 = 2. Табличное значение (табл. 9 П) χ ²_{(0.05, 2)} = 5.99.

Поскольку полученное значение (1.36) меньше табличного (5.99), нулевая гипотеза сохраняется, распределение бурозубок по массе тела достоверно от нормального не отличается.

Аналогичные расчеты для дискретного признака (плодовитость лисиц), имеющего предположительно биномиальное распределение (дискретный аналог нормального), представлены в табл. 7. Так, при параметрах M = 5 экз., S = 1.33 экз. для второго интервала получаем: t = |8 − 5| / 1.33 = 1.5.

Таблица 7

Центр интервала, xj	Фактическая частота, a	Нормиро­ванное от­клонение, t	Ординаты нормаль­ной кривой, p	Теорети­ческая частота, А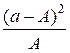
	1	2.26	0.031
		1.5	0.129
		0.75	0.301		0.05
			0.399
		0.75	0.301		0.94
		1.5	0.129
		2.26	0.031
Сумма	n = Σ a = 75			n = Σ A = 75	χ ² = 2

Соответствующая ордината нор­мальной кривой равна p = 0.1295 (графа 4), теоретическая частота составит:

А = с∙p = 56.38∙0.129 = 7.3 ≈ 7 (графа 5),

поскольку значение c = 1∙75/1.33 = 56.38. В результате вычислений получаем частоты (A) распределения (с параметрами М = 5, S = 1.33, n = 75), строго соответствующего биномиальному (см. рис. 5, с. 21). Объединим классы с частотами менее 4 и рассчитаем значение критерия χ ² = 2. Число степеней свободы (при трех ограничениях и пяти классах) равно df = 5 − 3 = 2. Поскольку это значение (χ ² = 2) меньше табличного (χ ²_{(0.05, 2)} = 5.99), нулевая гипотеза не может быть отклонена, значит, распределение лисиц по плодовитости в целом соответствует биномиальному закону.