1. На основании первичных данных составляется 4-хклеточная таблица следующего вида.
Таблица 34
| Замеры | Второй замер | Σ | ||
| Значения признака | Первый вариант ответа | Второй вариант ответа | ||
| Первый замер | Первый вариант ответа | A=f11 | B=f12 | A+B=f1– |
| Второй вариант ответа | C=f21 | D=f22 | C+D=f2– | |
| Σ | A+C=f11 | B+D=f11 | N |
В таблице 34 «А» обозначает число испытуемых, которые в первый и второй замеры выбрали первый вариант ответа; «С» — число испытуемых, которые в первый замер выбрали второй вариант ответа, а во второй замер выбрали первый вариант ответа; «В» — число испытуемых, которые в первый замер выбрали первый вариант ответа, а во второй замер — второй вариант ответа; «D» — число испытуемых, которые оба раза (в первый и второй замеры) выбрали второй вариант ответа.
Возможна ситуация, в которой В = С. В этом случае критерий Макнамары не может быть применен и следует воспользоваться критерием хи-квадрат.
2. Работа по критерию Макнамары начинается с выяснения вопроса о том, будет ли сумма чисел, стоящих в ячейках В и С, меньше или равна 20 или эта сумма будет превышать число 20. В первом случае, то есть когда сумма чисел В+С ≤ 20 используется один способ расчета по критерию — способ А. Если сумма чисел, стоящих в ячейках В + С > 20 — используется другой способ, способ Б.
Способ А. Пусть сумма (В + С) ≤ 20, тогда дальнейший расчет по критерию Макнамары производится следующим образом:
3. Находится наименьшая величина из величин В и С, которая обозначается буквой m, т.е т m=min (В или С).
3. Находится сумма величина В + С, которая обозначается буквой n, т.е. n= В + С.
4. По таблице приложения в данном пособии (таблицы критических значений биномиального распределения) на пересечении строк и столбцов таблицы m и n находится величина Мэмп.. Особо подчеркнем, что, в отличие от всех критериев, по таблице приложения 10 находятся не критические величины, а именно эмпирическое значение критерия Макнамары. Это принципиальное отличие этого критерия от всех других.
Примечание. Нули в таблице приложения 8 опущены, поэтому к любому числу, найденному по этой таблице, нужно слева добавить нуль и занятую, так чтобы получить необходимую величину в виде: 0,«число, взятое из таблицы».
5. Правило вывода:
Величины Мкрит. в случае способа А являются постоянными и равны соответственно Мкрит.=0,025 для 5% уровня значимости и Мкрит.=0,005 для 1% уровня значимости.
Если Мэмп. ≤ Мкрит., различия между замерами статистически значимы.
Если Мэмп. > Мкрит., различия между замерами статистически незначимы.
Способ Б. Пусть сумма (В + С) > 20.
3. Производится расчет Мэмп. по следующей формуле:
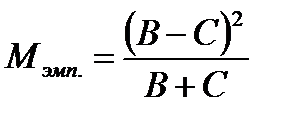
4. Правило вывода:
Находятся критические величины Мкрит. по таблице критических значений для критерия хи-квадрат с числом степеней свободы ν=1(для четырехпольных таблиц). Однако поскольку величина степени свободы критерия хи-квадрат в данном случае всегда постоянна и равна 1, то критические величины Мкрит. так же, как и в случае способа А, всегда одни и те же и равны Мкрит. =3,841 для 5% уровня значимости и Мкрит. = 6,635 для 1% уровня значимости.
Если Мэмп. ≥ Мкрит., различия между замерами статистически значимы.
Если Мэмп. < Мкрит., различия между замерами статистически незначимы.
 2015-04-20
2015-04-20 2080
2080
