§1.  Отображение и преобразование множеств.
Отображение и преобразование множеств.
Определение 1. Пусть Х и У непустые множества, Х´У – их декартово произведение
Х´У = {(х, у)|хÎХ, уÎУ}.
Рассмотрим подмножество G Ì Х´У. Если пара (х, у)ÎG, то говорят, что элементу х Î Х соответствует элемент у Î У относительно G.
При этом тройка f = (G, X, У) называется соответствием между множествами Х и У.
Пусть G = 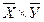 , где
, где 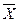 Ì Х,
Ì Х, 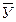 Ì У.
Ì У.
Тогда назовем 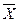 - областью определения соответствия f, а
- областью определения соответствия f, а 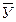 - областью значений соответствия f, при этом G – называется графиком соответствия f.
- областью значений соответствия f, при этом G – называется графиком соответствия f.
Определение 2. Соответствие f = (G, X, У) называется функцией, если для каждого значения хÎ 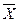 существует единственный элемент уÎУ такой, что пара (х, у)ÎG. При этом у называется значением функции f для элемента х и обозначают у = f(x) или элемент у = f(х) называется образом элемента х Î Х, а х - прообразом элемента уÎY.
существует единственный элемент уÎУ такой, что пара (х, у)ÎG. При этом у называется значением функции f для элемента х и обозначают у = f(x) или элемент у = f(х) называется образом элемента х Î Х, а х - прообразом элемента уÎY.
Если область определения функции f совпадает с множеством Х (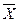 = Х), то говорят, что f есть отображение множества Х в множество У.
= Х), то говорят, что f есть отображение множества Х в множество У.
Эту функцию обозначают одной буквой, например f, и пишут так: f: Х®Y или Х f Y.
Вместо термина “функция” в геометрии принято говорить “отображение”, так как термин “функция” обычно употребляется для числовых множеств.
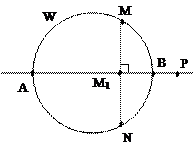 Например: Пусть W - окружность, а АВ - её диаметр. Каждой точке М окружности поставим в соответствие ортогональную проекцию М1 на прямую АВ.
Например: Пусть W - окружность, а АВ - её диаметр. Каждой точке М окружности поставим в соответствие ортогональную проекцию М1 на прямую АВ.
Получим отображение окружности W в прямую (АВ):
f 1 : W ® (АВ).
Если в отображении f: Х®Y множество Y = f (Х) = Х, то говорят, что дано отображение множества Х на себя.
Рассмотрим частные случаи отображений f: Х®Y.
1. Если для любых значений х1, х2 Î Х из условия х1 ¹ х2 следует
f(х1) ¹ f(х2), то отображение f называется инъективным или инъекцией Х в У.
2. Если полный образ множества Х совпадает с У, то есть Y = f (Х), то отображение f называется сюръективным или сюръекцией множества Х на У.
3. Если отображение f: Х®Y, одновременно, инъективное и сюръективное, то оно называется биективным или биекцией, или обратимым.
Преобразованием непустого множества Х называют любое биективное отображение множества Х на себя.
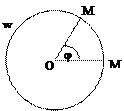
Например: Пусть W - окружность, заданная на ориентированной плоскости а j - ориентированный угол, причем -p<j£p отображение f: W®W, при котором каждой точке М окружности W ставится в соответствие точка М' - той же окружности такая, что ÐМОМ ' = j. Тогда f: W®W - преобразование окружности W.
ОБРАТНОЕ ОТОБРАЖЕНИЕ.
При отображении f: Х®Y каждый элемент множества Х переходит в один только один элемент из У. Но на элементы множества У ограничений не накладывается – в некоторые из них не отображается ни один из элементов множества Х, в другие ровно один элемент, а в некоторые несколько или даже бесконечно много элементов.
Определение 3. Назовем прообразом элемента у Î У при отображении f: Х®Y множество всех элементов из Х, которые при этом переходят в y.
Обозначаем прообраз:
f –1(y) = {x| xÎX Ù f(x) = y}.
Если рассматривать биективное отображение f: Х®Y, то нетрудно заметить, что каждый элемент у Î У имеет единственный прообраз. Это позволяет нам построить новое соответствие g: У®Х по закону
g(y) = x, если y = f(x).
Это соответствие называют обратным к f.
Замечание. Если мы рассматриваем биективное отображение f: Х®Y, то обратное соответствие g: У®Х также является биективным отображением. Однако для произвольного отображения f: Х®Y обратное соответствие g: У®Х может не быть даже отобажением. Возникает вопрос, когда же обратное соответствие g: У®Х является отображением? Во-первых, необходимо, чтобы каждый элемент у Î У имел прообраз, а, следовательно, отображение f: Х®Y должно быть сюръективным. Во-вторых, g(y) должно быть единственным элементом в Х, другими словами, каждый элемент у Î У имел прообраз, состоящий из одного элемента. Последнее утверждение говорит нам о том, что, отображение f: Х®Y должно быть инъективным. Таким образом, если отображение f: Х®Y – биекция, то обратное к f соответствие g: У®Х является отображением. Это обратное отображение принято обозначать f –1: У®Х.f –1 (y) = f –1 (f(x)) = x,
Определение 4. Под произведением g×f преобразований f, g Î Fх будем понимать g×f (х) = g (f (x)).
Очевидно, композиция f –1 × f: Х®Х является тождественным отображением.
Теорема 1. Если отображение f: Х®Y – биекция, то обратное к f отображение f –1: У®Х является также биективным отображением.
Доказательство. Покажем, что f –1: У®Х - сюръекция. Действительно, пусть y = f(x), тогда
f –1 (y) = f –1 (f(x)) = x,
то есть у прообраз х для f –1. Следовательно, f –1- сюръекция.
Покажем, что f –1: У®Х - инъекция. Действительно, выберем различные точки у1 ¹ у2, а их прообразы обозначим
х1 = f –1 (у1), х2 = f –1 (у2). Если предположить, что х1 = х2, то получим f(х1) = f(х2) и поэтому у1 = 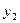 , что противоречит условию. Следовательно, х1 ¹ х2 и f –1: У®Х - биекция.
, что противоречит условию. Следовательно, х1 ¹ х2 и f –1: У®Х - биекция.
▄
Определение 5. Пусть f: Х®Х – преобразование множества Х. Элемент х Î Х (подмножество F Ì X) называется неподвижным или инвариантным элементом (подмножеством) для преобразования f, если f(x) = х (f(F) = F).
 2015-07-04
2015-07-04 1116
1116








