Говорят, что преобразование плоскости сохраняет расстояние, если расстояние между любыми двумя точками А и В плоскости равно расстоянию между их образами А' и B', т.е. |АВ| = |А'В'|.
Определение 6. Преобразование плоскости, сохраняющее расстояние, называется движением (или перемещением).
Наиболее простым примером движения является тождественное преобразование плоскости, т.е. преобразование, при котором каждая точка плоскости переходит в себя.
Рассмотрим примеры движений.
1. Параллельный перенос.
Возьмем вектор 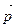 , параллельный плоскости s. Каждой точке М Î s поставим в соответствие точку М¢ так, чтобы
, параллельный плоскости s. Каждой точке М Î s поставим в соответствие точку М¢ так, чтобы 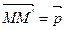 . Мы получаем некоторое отображение f: s ® s, которое является преобразованием плоскости s. Оно называется параллельным переносом на вектор
. Мы получаем некоторое отображение f: s ® s, которое является преобразованием плоскости s. Оно называется параллельным переносом на вектор 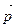 . Вектор
. Вектор 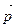 называется вектором переноса.
называется вектором переноса.
Если 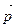 =0, то параллельный перенос - есть тождественное преобразование.
=0, то параллельный перенос - есть тождественное преобразование.
Докажем, что параллельный перенос является движением.
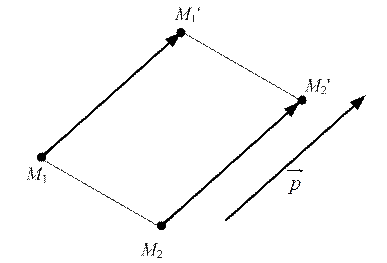
Пусть М1 и М2 - две точки плоскости, а М1' и М2' - их образы. Тогда 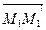 =
= 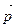 ,
, 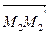 =
= 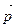 , поэтому
, поэтому 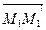 =
= 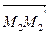 . Согласно лемме о равенстве векторов, имеем
. Согласно лемме о равенстве векторов, имеем 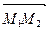 =
= 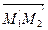 и, следовательно, | M1M2 | = | М1' М2 '|. Таким образом при параллельном переносе сохраняются расстояния, т.е. параллельный перенос является движение.
и, следовательно, | M1M2 | = | М1' М2 '|. Таким образом при параллельном переносе сохраняются расстояния, т.е. параллельный перенос является движение.
▄
В дальнейшем будем обозначать параллельный перенос 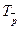 . Рассмотрим на плоскости прямоугольную декартовую систему координат О
. Рассмотрим на плоскости прямоугольную декартовую систему координат О  и зададим координатами точки М(х,у), М’(x’,y’) и вектор
и зададим координатами точки М(х,у), М’(x’,y’) и вектор 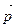 (a,b). Тогда
(a,b). Тогда
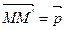 Þ
Þ 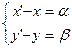 Þ
Þ 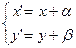 .
.
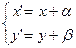 . (1)
. (1)
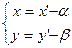 . (2)
. (2)
Формулы (1) будем называть формулами параллельного переноса  .
.
 2015-07-04
2015-07-04 1435
1435
