Осевая симметрия.

Определение 7. Пусть имеем прямую 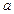на плоскости. Точки М и М' называются симметричными относительно прямой 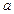, если отрезок ММ¢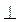 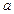, а его середина М₀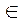 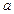. Если точка М ,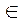

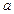Если точка М 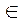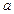, то она называется симметричной сама себе относительно прямой .

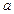Определение 8. Преобразование плоскости, которое каждой точке ставит в соответствие симметричную ей точку относительно прямой 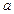, называется осевой симметрией с осью .

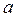Осевую симметрию обозначим S .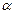

Выберем прямоугольную декартову систему координат, для которой ось 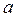является осью абсцисс.

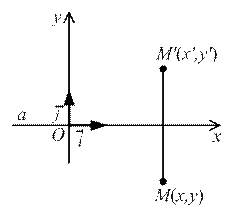
Тогда

S_a: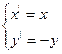

формулы осевой симметрии в этой системе координат.

Формулы обратного преобразования будут иметь вид

S : ,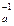

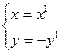т.е. формулы для обратного преобразования имеют один и тот же вид. Следовательно, это есть одно и то же преобразование:

S_a= S .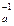

Таким образом, осевая симметрия является инвалютивным преобразованием плоскости.

Из уравнения осевой симметрии следует, что неподвижными точками будут только точки, у которых ордината равна нулю. Значит, все точки оси симметрии неподвижны.

Очевидно, что ось симметрии - неподвижная прямая. Она отображается сама в себя.

Пусть прямая ℓ задана уравнением

ℓ: Ax + By + C = 0.

Тогда ее образ имеет уравнение

S 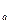(ℓ): Ax¢ – By¢ + C = 0.

Прямая ℓ будет отображаться в себя при В=0. Это будут прямые, перпендикулярные оси симметрии а. Однако, каждая точка этой прямой не является неподвижной.

3. Поворот плоскости.

Пусть на ориентированной плоскости заданы направленный угол a и точка О.

Определение 9. Преобразование плоскости, заданное следующими условиями:

1) образом точки О является сама точка О,

2) если образом точки М (М¹О) является точка М¢, то

|OM| = |OM’| и Ð MOM¢ = a

называется поворотом плоскости на угол a вокруг точки О.

В дальнейшем пользуемся следующим обозначением поворота вокруг центра О на угол a: R .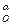

Замечание. Если мы имеем два поворота вокруг точки О на угол a и угол a ¢, где

a ¢ = ,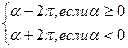

то эти повороты совпадают.

Следовательно, угол поворота можно рассматривать в промежутке [ ].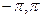

Аналитическое задание поворота.

Пусть в прямоугольной декартовой системе координат O задан поворот вокруг точки О на угол :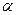

М ¹ О, М(х, у), М¢(x¢, y¢), Ð ХOM = 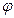, ÐMOM¢ = a.

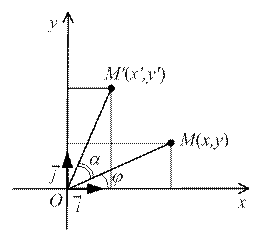
Тогда имеем:

,

,

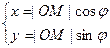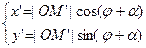Известно, что

|OM| = |OM¢|,

поэтому получим

.

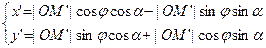Сделав замену, приходим к формулам

. (1)

Формулы (1) определяют поворот плоскости на угол a вокруг точки О в системе координат O .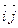

Замечание. Поворот на угол a = 0 есть тождественное преобразование плоскости.

Действительно, формулы (1) принимаю вид

.

4. Центральная симметрия.

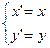Определение 10. Точки М и М^' называются симметричными относительно точки О, если О - середина отрезка ММ'. Точка О симметрична сама себе.

Определение 11. Преобразование плоскости, которое каждую точку отображает в симметричную ей точку относительно центра О называется центральной симметрией с центром в точке О и обозначается Z₀.

Очевидно, что центральная симметрия есть поворот вокруг точки О на угол 180⁰. Поэтому формулы центральной симметрии получим из формул поворота:

Z_o: .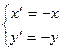

В центральной симметрии неподвижная точка только одна. Это центр симметрии. А неподвижными прямыми являются прямые, проходящие через центр симметрии. Заметим, что

,

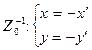то есть формулы прямой и обратной центральных симметрий имеют один и тот же вид. Следовательно, центральная симметрия также является инвалютивным преобразованием плоскости.