Найдем формулы аффинного преобразования в произвольной аффинной системе  координат О
координат О 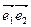 . Для этого рассмотрим на плоскости две аффинные системы
. Для этого рассмотрим на плоскости две аффинные системы  координат R = (О
координат R = (О 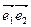 ) и R¢ = (О’
) и R¢ = (О’ 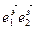 ). Назовём R - старой системой координат, а R¢ – новой системой координат. Пусть М – произвольная точка плоскости, имеющая в R координаты (х, у), а в R¢ координаты (х¢, у¢). Наша задача найти формулы, позволяющие выразить старые координаты точки M через её новые координаты.
). Назовём R - старой системой координат, а R¢ – новой системой координат. Пусть М – произвольная точка плоскости, имеющая в R координаты (х, у), а в R¢ координаты (х¢, у¢). Наша задача найти формулы, позволяющие выразить старые координаты точки M через её новые координаты.
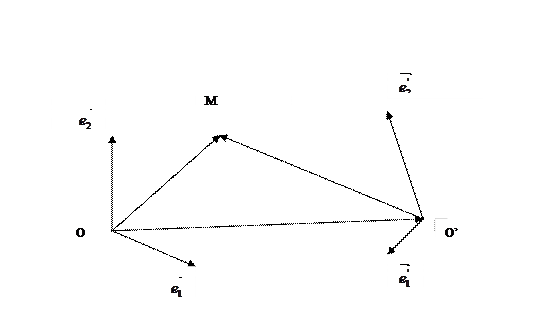
Пусть в старой системе координат R = (О 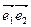 ) задана точка O¢ (c1, c2) и базисные вектора
) задана точка O¢ (c1, c2) и базисные вектора 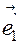 (а
(а 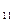 ,а
,а 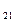 ),
), 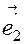 (а
(а 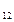 ,а
,а  ).
).
Тогда получим
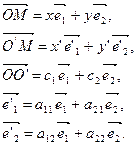 (*)
(*)
Из треугольника 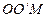 имеем:
имеем:
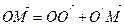
 2015-07-04
2015-07-04 1323
1323








