{ 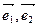 } согласно формулам (*) получим
} согласно формулам (*) получим
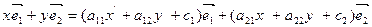 .
.
Из этого равенства, в силу единственности разложения вектора по базисным векторам находим:
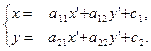 (1) (1)
(1) (1)
Полученную зависимость (1) между старыми и новыми координатами точки М называют формулами преобразования аффинной системы координат.
Следствие: Движение и подобие являются частными случаями аффинных преобразований в силу их соответствующих аналитических заданий.
Рассмотрим частные случаи полученного нами выше преобразования системы координат.
1. Перенос начала координат. В этом случае координатные реперы R и R¢ имеют одни и те же координатные векторы, но разные начала координат. Поэтому
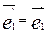 ,
, 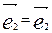 ,
, 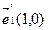 ,
, 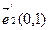
а 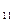 =1, а
=1, а 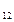 =0, а
=0, а 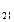 =0, а
=0, а 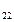 =1
=1
Формулы (1) принимают вид
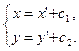 (2)
(2)
и при этом говорят, что “новая” система координат R¢ = (О’ 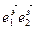 ) получена из “старой” R = (О
) получена из “старой” R = (О 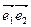 ) параллельным переносом.
) параллельным переносом.
2. Замена координатных векторов. В этом случае координатные реперы R и R¢ имеют одно начало, но разные базисные вектора.
Поэтому с 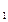 = с
= с 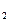 = 0.
= 0.
Формулы (1) принимают вид:
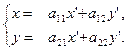 (3)
(3)
и при этом говорят, что “новая” система координат R¢ = (О’ 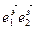 ) получена из “старой” R = (О
) получена из “старой” R = (О 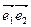 ) поворотом осей координат.
) поворотом осей координат.
Пусть задано аффинное преобразование плоскости реперами f: R®R’. Пусть произвольная точка М плоскости имеет координаты (х, у), а ее образ точка М¢ в R имеет координаты (х¢, у¢). Тогда точка М¢ в новом репере R¢ имеет координаты (х, у). Итак, мы можем рассматривать точку М¢ одновременно в двух системах координат: старой R и новой R¢ одновременно и поэтому на координаты точки М¢ смотреть с точки зрения новых и старых координат как в предыдущем пункте. Обратим внимание на то, что старые координаты стали обладать штрихами, а новые координаты их потеряли. При этом мы получили связь между координатами точки М и ее образа М¢ и эта связь дает нам искомые формулы аффинного преобразования
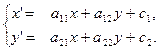
Матрица, составленная из коэффициентов при переменных x, y, является матрицей перехода от репера R к реперу R¢, поэтому ее определитель отличен от нуля. Если определитель матрицы больше нуля, то мы имеем аффинное преобразование первого рода, а если определитель матрицы меньше нуля, то мы имеем аффинное преобразование второго рода.
Как видим, полученные ранее формулы подобия и движения плоскости являются частным случаем формул аффинного преобразования плоскости.
 2015-07-04
2015-07-04 634
634








