2015-07-04
317
Предположим, что с данным случайным экспериментом связана полная группа событий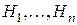 
, вероятности которых 
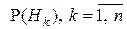известны. Нас интересует некоторое событие А, которое может наступить одновременно с одним из событий 
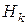. При этом условные вероятности 
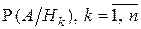наступления события А при каждом 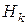известны. Требуется определить безусловную вероятность 
.
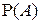Представим событие А в виде:
.
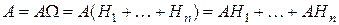В последней сумме слагаемые являются попарно несовместными: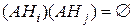 
. Поэтому, используя аксиому аддитивности и правило умножения вероятностей, получаем:
.
Формула
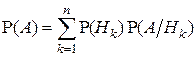
называется формулой полной вероятности. В ней события 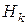называются гипотезами (так как одно из 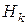обязательно происходит), а 
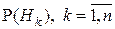- вероятностями гипотез.
Пусть, по-прежнему, со случайным экспериментом связано n гипотез 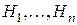, вероятности которых 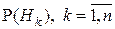известны. Известно также, что гипотеза 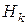сообщает событию А вероятность 
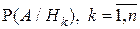. Предположим, что эксперимент был произведён, и в результате событие А произошло. Этот факт приводит к переоценке вероятностей гипотез 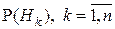. Количественно этот вопрос решает следующая формула:
.
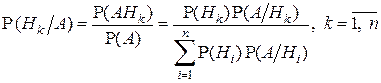Полученная формула называется формулой Байеса (или формулой гипотез). В ней 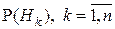называются априорными вероятностями гипотез (они определяются a priori – до проведения опыта). Условные вероятности 
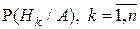называются апостериорными вероятностями гипотез (они вычисляются a posteriori – после проведения опыта, когда стало известно, что событие А произошло).
Пример. По каналу связи с помехами передаются двоичные символы {0,1}. Вероятности искажения символов в канале (0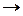 
1, 1 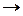0) одинаковы и равны 0.2. Вероятность символа 0 на входе канала равна 0,9, а вероятность символа 1 - 0,1. На выходе канала принят сигнал, соответствующий 1. Определить вероятность того, что на вход каналаподавалась также 1.
Решение.
Рассмотрим гипотезы
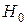= {На входе канала связи символ 0},
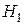= {На входе канала связи символ 1}.
Очевидно,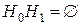 
и по условию 
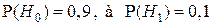, то есть события 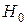и 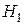образуют полную группу событий.
Пусть событие А = {На выходе канала принят символ 1}.
По условию задачи вероятность искажения символа 0 в канале суть условная вероятность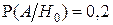 
, а условная вероятность 
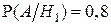является вероятностью неискажения в канале символа 1. В терминах введенных обозначений требуется найти условную (апостериорную) вероятность 
.
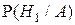Найдем вначале по формуле полной вероятности безусловную вероятность события А:
.
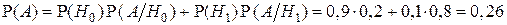Затем, в соответствии с формулой Байеса, находим апостериорную вероятность :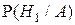
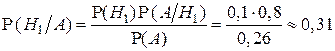
(при априорной вероятности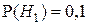 
).
Очевидно, что при этом апостериорная вероятность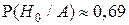 
(при априорной вероятности 
).
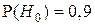Замечание. Таким образом, даже при приеме на выходе канала связи 1 мы отдаем предпочтение в пользу 0 на входе. Это объясняется тем, что априорная вероятность 0 на входе канала существенно больше априорной вероятности 1.
