2015-07-04
1607
Функция вида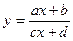 
, где 
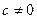и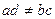 
, называется дробно-линейной. Графиком этой функции является гипербола.
Частным случаем дробно-линейной функции является функция обратной пропорциональности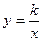 
. График этой функции состоит из двух ветвей, симметричных относительно начала координат. При 
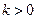гипербола расположена в первой и третьей четвертях, при 
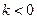– во второй и четвертой четвертях.
Пример 11. Постройте график функции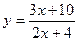 
.
Решение. Выделим целую часть дроби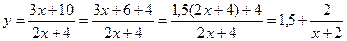 
.
Таким образом, уравнение, которым задается график функции, примет вид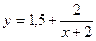 
. График заданной функции получается из графика функции 
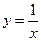сдвигом на 2 единицы по оси OX влево, растяжением вдоль оси OY в 2 раза и сдвигом на 1,5 единицы по оси OY вверх.
Заметим, что график функции не пересекает прямые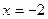 
и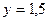 
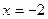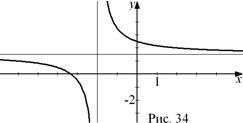
, хотя и приближается к ним достаточно близко. Такие прямые называются асимптотами графика функции. График дробно-линейной функции имеет две асимптоты – вертикальную и горизонтальную 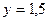. Построение графика удобно начинать именно с нахождения асимптот: для нахождения вертикальной асимптоты приравниваем знаменатель дроби нулю, а для нахождения горизонтальной асимптоты выделяем целую часть дроби (рис. 34).
|
|
|
Построение графика произвольной дробно-линейной функции 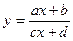выполняется по алгоритмам, разобранным в примере 11.
