2015-07-04
757
Над прямоугольной декартовой системой координат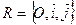 
выполнили преобразование и получили систему 
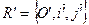. Для прямоугольных координат справедливы формулы (2.3)-(2.5).
Рассмотрим подробнее преобразование координатных ортов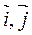 
.
Поворот прямоугольной системы координат на угол α
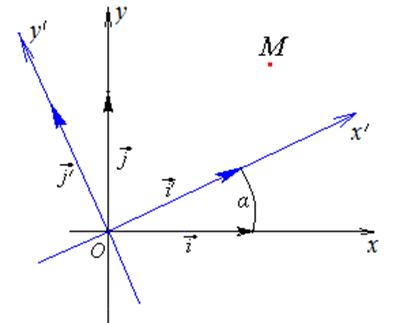
Найдем «старые» координаты ортов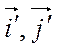 
для того, чтобы подставить в формулы (2.3).
Пусть α – угол между векторами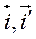 
.
Тогда координаты векторов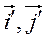 
в базисе (
):
|
= 
, 
= 
.
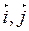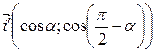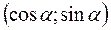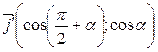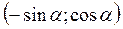Подставим в формулы (2.3):
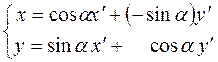или 
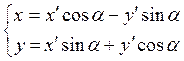(2.6)
В матричной форме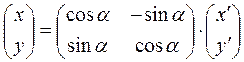 
.
Это формулы поворота осей прямоугольной системы координат.
Причем
.
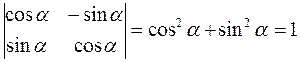В обеих системах координат 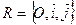и 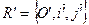движение от первого вектора ко второму совершается против часовой стрелки, т.е. в одинаковом положительном направлении. Говорят, что системы не меняют своей ориентации (в рассмотренном случае обе – правые).
