2015-07-04
1048
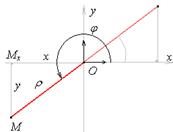
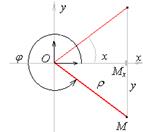
Пусть дана система координат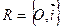 
, в которой М (r; j.). Присоединим к полярной системе координат прямоугольную декартову 
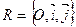, где М (х; у).
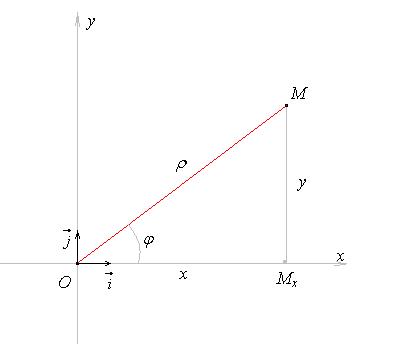
Задача: известны полярные координаты точки М. Найдем прямоугольные.
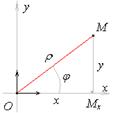
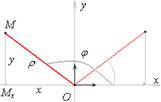
Рассмотрим треугольник ОМхМ: ОМх=х, ММх=у, ОМ=r, Ð МхОМ=j.
, 
,
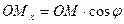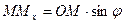т.е.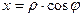 
, 
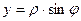. (1)
Пусть 0< j <2 p, r ³0. Тогда
| Положение точки М (х; у) в системе координат | Знаки координат | Знаки косинуса, синуса | Формула для х | Формула для у |
I четверть
0< j < p /2
| х >0, у >0 | cos j >0 sin j >0 |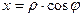
|
|
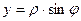
II четверть
p /2< j < p
| х <0, у >0 | cos j <0 sin j >0 |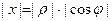 
|
|
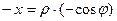
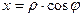
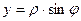
III четверть
p < j <3 p /2
| х <0, у <0 | cos j <0 sin j <0 |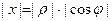
| 
|
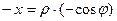
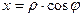
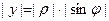
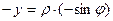
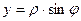
IV четверть
3 p /2< j <2 p
| х >0, у <0 | cos j >0 sin j <0 |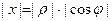
|
|
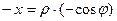
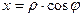
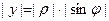
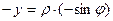
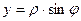
Обратная задача.
Известны прямоугольные координаты точки М. Найдем полярные.
.
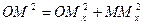Отсюда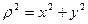 
, т.е. 
,
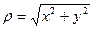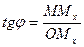, т.е. 
.
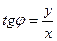Получили:
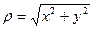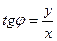, (2)
Аналогичные формулы можно вывести для обобщенных полярных координат.
, .
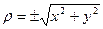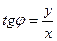Пример 2.
Дано: А (1; 1)
Найти: полярные координаты точки А.
Решение.
По формулам (2):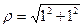 
= 
, 
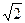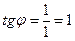, т.е.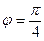 
Значит, полярные координаты точки А (;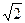 
).
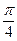Ответ: А (; ).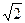
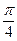Пример 3.
Дано: А (2;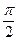 
)
Найти: декартовы координаты точки А.
Решение.
По формулам (1):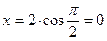 
, 
.
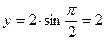Ответ: А (0; 2)
