Метод координат в плоскости
Определение 7.
Тройка 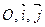 называется прямоугольной (декартовой) системой координат в плоскости или прямоугольным репером.
называется прямоугольной (декартовой) системой координат в плоскости или прямоугольным репером.
Обозначается 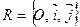 .
.
Метрические задачи
Задача 9. Вычисление площади треугольника
Дано: 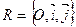 , А (х 1; у 1), В (х 2; у 2), С (х 3; у 3).
, А (х 1; у 1), В (х 2; у 2), С (х 3; у 3).
Найти: площадь треугольника АВС.
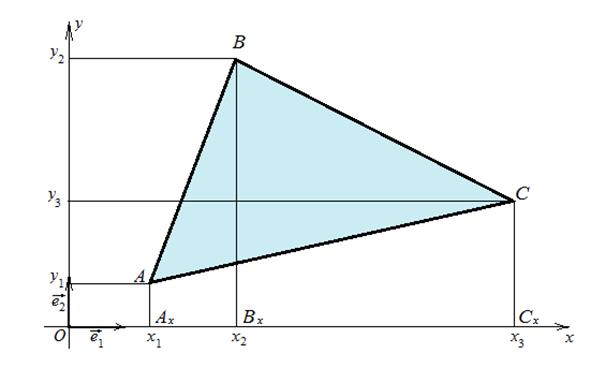
Решение (рис.1.14).
|
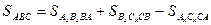 .
.
Вычислим площади трапеций АхВхВА, ВхСхСВ, АхСхСА по формуле 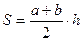 :
:
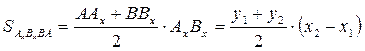 ,
,
аналогично 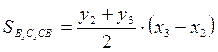 ,
, 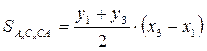 .
.
Тогда 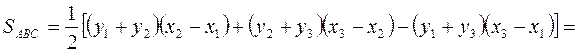
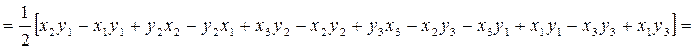
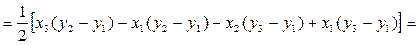
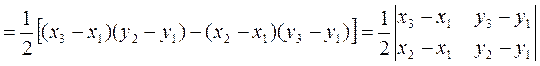 .
.
Точки А, В и С могут располагаться иначе, а определитель, составленный из их координат – положительным или отрицательным числом, поэтому
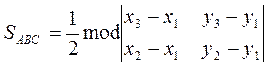 . (2.1)
. (2.1)
Если точки А, В и С лежат на одной прямой, то S =0 и, наоборот.
Пример 7.
Дано: А (6; 0), В (–2; 1), С (2; 7).
Найти: 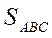 .
.
Решение.
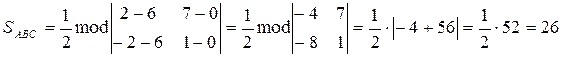 .
.
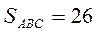 .
.
Преобразование координат в плоскости
Преобразование аффинных координат
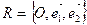 ®
® 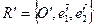 .
.
Назовем систему координат 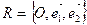 «старой», а
«старой», а 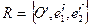 – «новой».
– «новой».
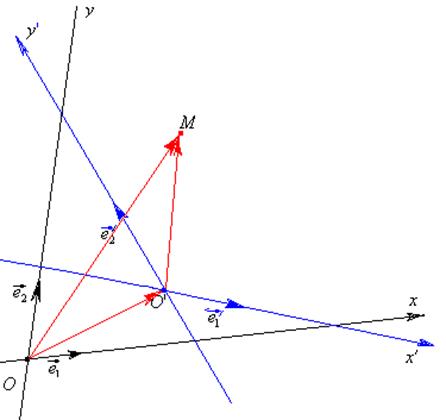
Пусть точка М имеет в R координаты М (х; у), т.е. ей соответствует радиус-вектор 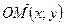 . Пусть точка М имеет в R ¢ координаты М (х ¢; у ¢), т.е. ей соответствует радиус-вектор
. Пусть точка М имеет в R ¢ координаты М (х ¢; у ¢), т.е. ей соответствует радиус-вектор 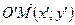 . Найдем зависимость между «старыми» и «новыми» координатами точки М.
. Найдем зависимость между «старыми» и «новыми» координатами точки М.
Радиус-векторы точек связаны равенством:
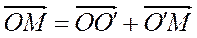 . (2.2)
. (2.2)
Рассмотрим координаты точек и векторов в обеих системах координат.
В «старой» системе:
точка О ¢(a; b) Þ 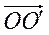 (a; b) Þ
(a; b) Þ 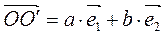 ,
,
векторы 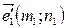 Þ
Þ 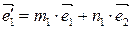
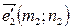 Þ
Þ 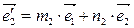 ,
,
точка М (х; у) Þ 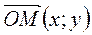 =
= 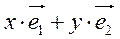 .
.
В «новой» системе:
точка М (х ¢; у ¢) Þ 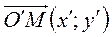 =
= 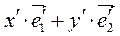 .
.
Из равенства (2.2) получаем:
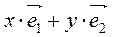 =(
=(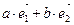 )+(
)+(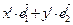 )=(
)=(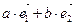 )+[
)+[ 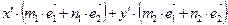 ],
],
т.е. 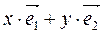 =
= 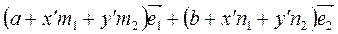 .
.
Из единственности разложения вектора по базисным векторам – координатным ортам 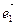 ,
, 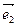 и по определению координат получаем:
и по определению координат получаем:
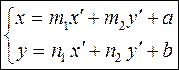 (2.3)
(2.3)
или в матричной форме 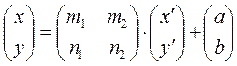 (2.3*).
(2.3*).
Формулы (2.3) связывают «старые» и «новые» координаты точки М при преобразовании аффинной системы координат в другую аффинную систему координат.
Для того чтобы решить обратную задачу: найти новые координаты по известным старым, следует разрешить систему уравнений (2.4) относительно неизвестных х ¢; у ¢.
Рассмотрим частные случаи.
1) Перенос начала координат (параллельный перенос системы координат на вектор 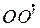 ). Это означает, что изменяется положение начала координат и сохраняется направление координатных осей, т.е. координатные векторы,
). Это означает, что изменяется положение начала координат и сохраняется направление координатных осей, т.е. координатные векторы, 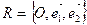 ®
® 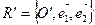 .
.
 2015-07-04
2015-07-04 3334
3334