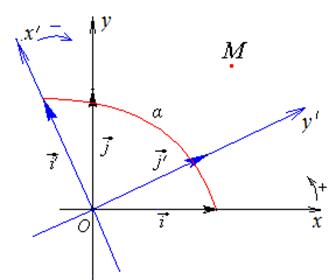
Рассмотрим случай, когда система 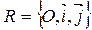 ориентирована положительно (правая), а система
ориентирована положительно (правая), а система 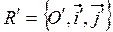 – отрицательно (левая), т.е. в ней движение от первого вектора ко второму совершается по часовой стрелке.
– отрицательно (левая), т.е. в ней движение от первого вектора ко второму совершается по часовой стрелке.
Угол α – угол между векторами 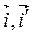 , тогда по формулам приведения координаты векторов
, тогда по формулам приведения координаты векторов 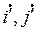 в базисе (
в базисе (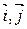 ) следующие:
) следующие:
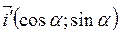 ,
, 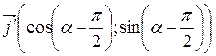 =
= 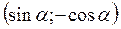 .
.
Формулы (2.3) примут вид:
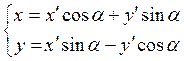 (2.7)
(2.7)
В матричной форме 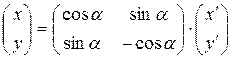 .
.
Причем 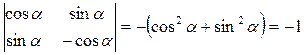 .
.
Формулы (2.6)-(2.7) можно объединить:
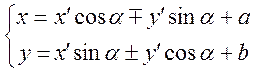 (2.8) или
(2.8) или 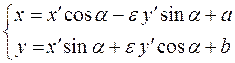 , (2.9)
, (2.9)
где e =1, если системы обе правые или левые, говорят, ориентированы одинаково, e =–1, если системы ориентированы противоположно.
Пример 8.
Дано: 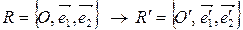 .
.
O ¢(2;5), 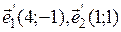 – «старые» координаты.
– «старые» координаты.
Найти: формулы преобразования координат.
Решение.
Подставим в формулы (2.3): 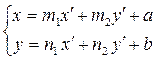 «старые» координаты нового начала и координатных векторов:
«старые» координаты нового начала и координатных векторов: 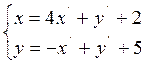 .
.
 2015-07-04
2015-07-04 468
468








