Положение точки на плоскости можно определять по двум координатам: паре чисел. Это не единственный способ. Кроме аффинной и прямоугольной системы применяют систему полярных координат.
Зададим ориентированную плоскость. Выберем точку О, луч р с началом в этой точке и единичный вектор 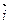 .
.

Определение.
Пара О, 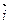 называется полярной системой координат, обозначается
называется полярной системой координат, обозначается 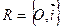 . Точка О называется полюсом, луч Ор – полярной осью.
. Точка О называется полюсом, луч Ор – полярной осью.
Полярная система координат может быть определена также парой точек О и Е: 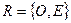 .
.

Рассмотрим произвольную точку плоскости – точку М. Ее положение определяется расстоянием от точки О, ОМ = r и углом j между лучами Ор и ОМ.
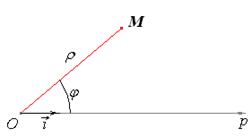
Вектор 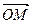 называют радиус-вектором точки М, отрезок ОМ=r – полярным радиусом точки М (r ³0), угол j – полярным углом точки М (
называют радиус-вектором точки М, отрезок ОМ=r – полярным радиусом точки М (r ³0), угол j – полярным углом точки М (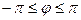 или
или 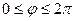 ).
).
Произвольная точка плоскости определяется парой r и j. Для полюса (М = О) r =0, j – любой (иногда указывают конкретное значение, например, j= 0).
Определение.
Пара чисел (r; j.) в полярной системе координат 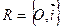 называется полярными координатами точки плоскости, обозначается М (r; j.)
называется полярными координатами точки плоскости, обозначается М (r; j.)
Пример 1.
Построить точки 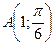 ,
, 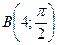 ,
, 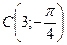 ,
, 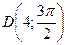 .
.
 2015-07-04
2015-07-04 784
784








