2015-07-04
896
Определение. Аффинным репером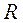 
на плоскости называют упорядоченную тройку точек О, А 1, А 2 плоскости, не лежащих на одной прямой.
Если на плоскости задан аффинный репер R={ О, А 1, А 2},то говорят что на плоскости задана аффинная система координат.
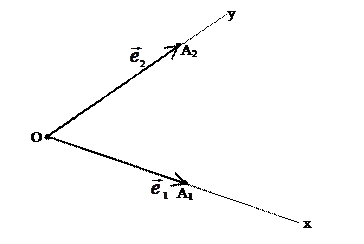
Рис. 1.
Точка О называется началом системы координат. Векторы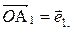 
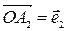, образующие неколлинеарную систему векторов являются базисом пространства V2 и называются базисными векторами данной системы координат или базисом данного репера R={ О, А 1, А 2}. Таким образом, репер R={ О,А 1, А 2}, можно задавать точкой О и базисными векторами 
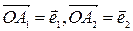. В этом случае аффинная система координат на плоскости обозначается R=(О 
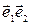). Векторы 
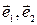называют координатными или базисными векторами аффинной системы координат (
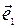-первый координатный вектор, 
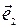- второй). Направленные прямые, проходящие через начало координат и параллельные координатным векторам, на которых положительные направления определяются этими векторами, называются координатными осями. Оси, параллельные векторам 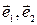, называются соответственно осями абсцисс и ординат и обозначаются так: 
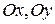. Иногда систему координат О 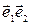обозначают через Оху.
|
|
|
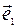
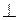
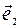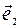
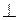
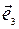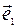
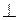
Есл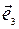и 
; 
; и │ 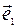│=│ │=│ 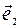│= 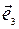1, то репер называют прямоугольным, а систему координат называют прямоугольной или декартовой системой координат и обозначают R = (O, 
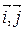), где │ 
│=│ 
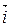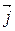│. В этом случае система координат изображается следующим образом.
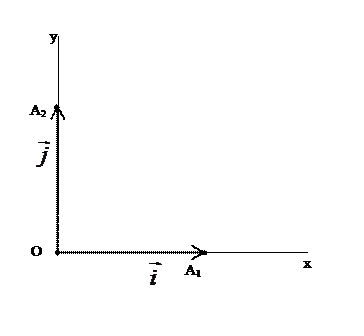
Рис. 2.
