2015-07-03
2084
Пример 3(а). Дан треугольник с вершинам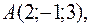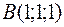и 
и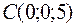 
. Найти его внутренний угол при вершине 
.
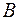А
С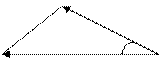 
В
Для нахождения внутреннего угла при вершине 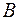воспользуемся формулой:
.
;
. 
;
;
.
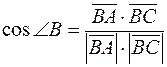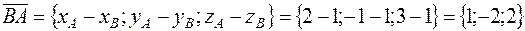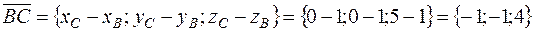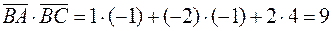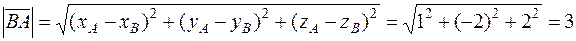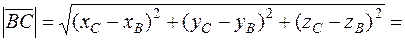
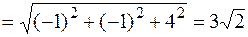Следовательно,
.
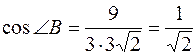Тогда
.
Пример 3(б). Доказать, что точк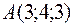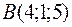и 
, 
и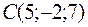 
лежат на одной прямой.
А В С
Найдём координаты векторов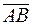 
и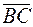 
:
;
.
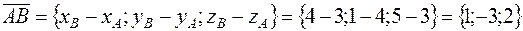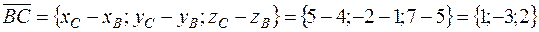Так как векторы 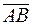и 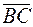имеют общую точку 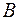, то достаточно доказать, что векторы 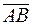и 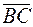коллинеарны.
Для доказательства воспользуемся условием коллинеарности векторов. У коллинеарных векторов координаты пропорциональны.
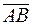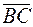Координаты векторов и пропорциональны, так как
.
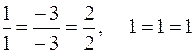Тогда векторы 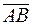и 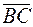коллинеарны. Отсюда следует, что точки 
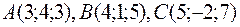лежат на одной прямой.
Пример 3(в). Доказать, что точк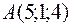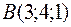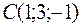и 
, 
, 
и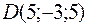 
являются вершинами трапеции.
А В
D 
С
Для того чтобы четырёхугольник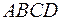 
являлся трапецией, надо, чтобы у него две противолежащие стороны были параллельны, а две другие противолежащие стороны нет. Кроме того, вершины 
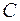и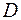 
должны быть расположены так, чтобы векторы 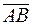и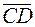 
имели противоположное направление.
Для доказательства воспользуемся условием коллинеарности векторов. У коллинеарных векторов координаты пропорциональны.
Найдём координаты векторов, совпадающих со сторонами четырёхугольника:
;
;
;
.
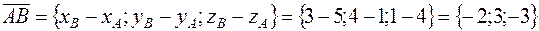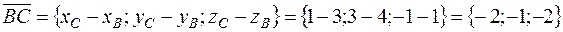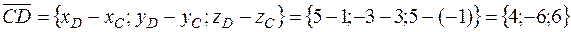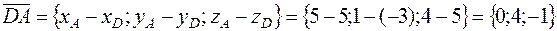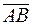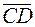Координаты векторов и пропорциональны, так как
.
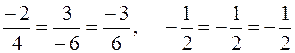Тогда векторы 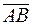и 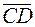коллинеарны. Отсюда следует, что противолежащие стороны 
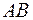и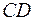 
четырёхугольника 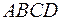параллельны.
Так как коэффициент пропорциональности векторов 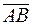и 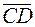равен – 
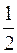, то векторы 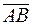и 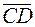имеют противоположное направление.
Координаты векторов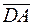 
и 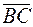не пропорциональны, так как
.
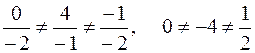Тогда векторы 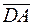и 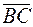не коллинеарны. Отсюда следует, что противолежащие стороны 
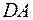и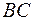 
четырёхугольника 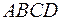не параллельны.
Следовательно, четырёхугольник 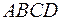является трапецией.
Пример 3(г). Доказать, что диагонали четырёхугольника с вершинам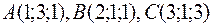и 
и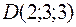 
взаимно перпендикулярны.
В
|
|
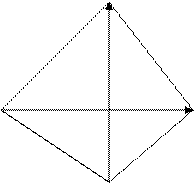
D
Диагоналям в четырёхугольнике 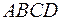соответствуют векторы 
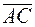и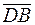 
. Векторы 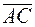и 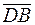будут перпендикулярны, если скалярное произведение этих векторов будет равняться нулю. То есть векторы 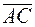и 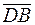будут перпендикулярны, если будет выполняться равенство 
.
Для доказательства найдём координаты векторов 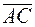и :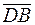
;
.
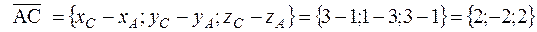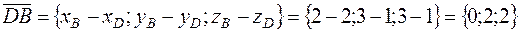Найдём скалярное произведение векторов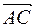 
и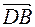 
:
.
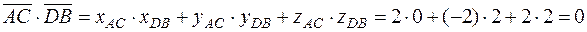Получили, что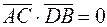 
. Из чего следует, что диагонали четырёхугольника 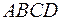, соответствующие векторам 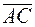и 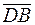перпендикулярны.
