«Если функция G(x) кусочно- непрерывна на [0;1], то тригонометрический ряд (2) с коэффициентами Фурье (3):
(1) сходится на всей числовой оси 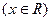 и определяет на R периодическую функцию S(x) (сумму ряда) с периодом Т=1:
и определяет на R периодическую функцию S(x) (сумму ряда) с периодом Т=1: 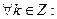 S(x+k) =S(x);
S(x+k) =S(x);
(2) на промежутке [0;1] ряд сходится к функции G(x) «в среднем»:
- 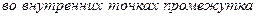 его сумма S(x) равна полусумме односторонних пределов функции G(x)
его сумма S(x) равна полусумме односторонних пределов функции G(x)
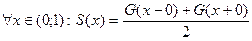
- 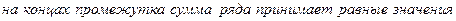
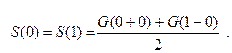
(3) Частичная сумма ряда Фурье 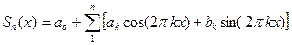 определяет тригонометрический многочлен наилучшего среднеквадратического приближения функции G(x) на промежутке [0;1], причем среднеквадратическое отклонение СКО этого многочлена от функции СКО=
определяет тригонометрический многочлен наилучшего среднеквадратического приближения функции G(x) на промежутке [0;1], причем среднеквадратическое отклонение СКО этого многочлена от функции СКО= 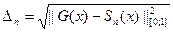 определяется соотношениями:
определяется соотношениями:
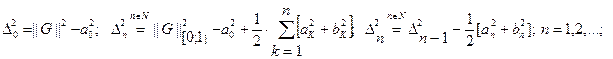
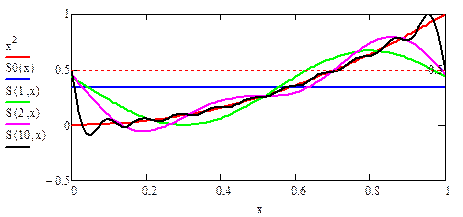
Пример: тригонометрический ряд Фурье для функции g(x)=x2 на [0;1]
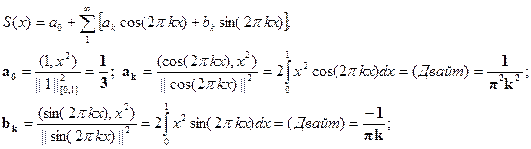
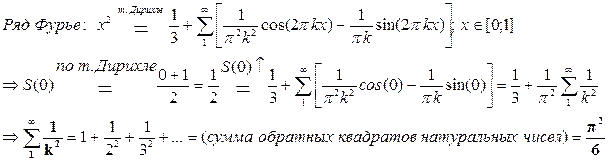
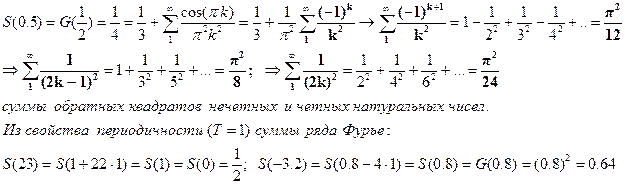
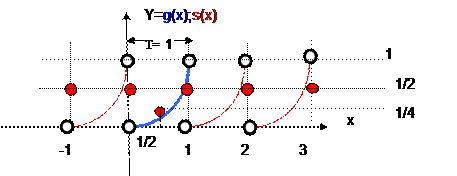
График суммы ряда Фурье для функции g(x)=x2 на [0;1].
Построим тригонометрические многочлены наилучшего с.к. приближения функции G(x)=x2 на [0;1] и вычислим соответствующие С.К.О.
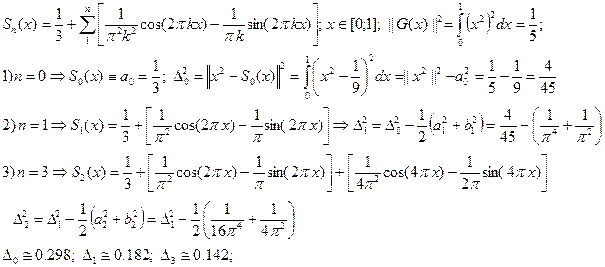
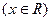 и определяет на R периодическую функцию S(x) (сумму ряда) с периодом Т=1:
и определяет на R периодическую функцию S(x) (сумму ряда) с периодом Т=1: 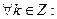 S(x+k) =S(x);
S(x+k) =S(x);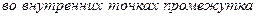 его сумма S(x) равна полусумме односторонних пределов функции G(x)
его сумма S(x) равна полусумме односторонних пределов функции G(x)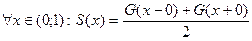
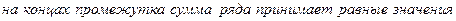
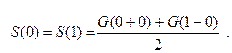
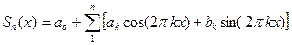 определяет тригонометрический многочлен наилучшего среднеквадратического приближения функции G(x) на промежутке [0;1], причем среднеквадратическое отклонение СКО этого многочлена от функции СКО=
определяет тригонометрический многочлен наилучшего среднеквадратического приближения функции G(x) на промежутке [0;1], причем среднеквадратическое отклонение СКО этого многочлена от функции СКО= 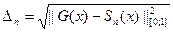 определяется соотношениями:
определяется соотношениями: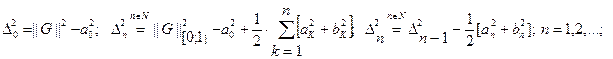
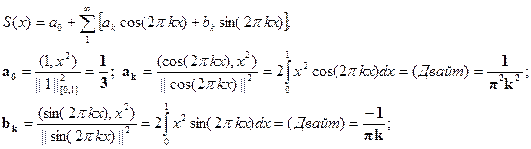
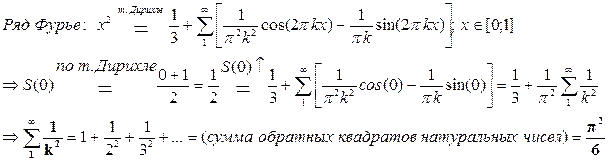
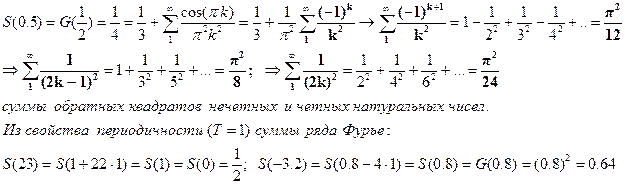
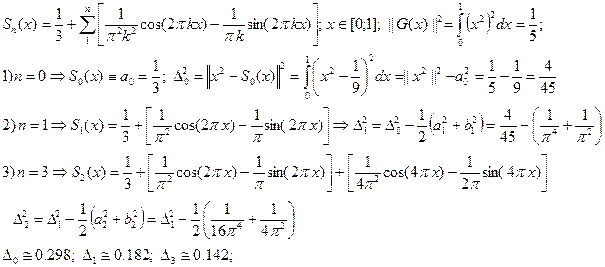
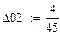
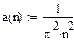
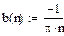
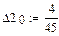
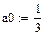
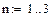
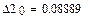
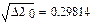
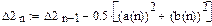
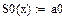
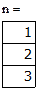
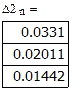
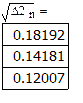
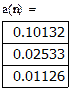
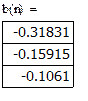
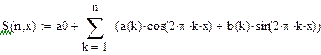
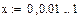
 2015-07-03
2015-07-03 769
769







