Скалярным произведением (СП) функций 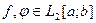 называется число
называется число
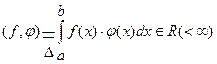 (2)
(2)
Свойства скалярного произведения: 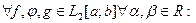
1) (f,φ) = (φ,f); 2) 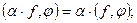 3)
3) 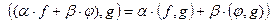
Определение 3. Нормой функции f 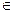 L2[a;b], «порожденной скалярным произведением», называется неотрицательное число
L2[a;b], «порожденной скалярным произведением», называется неотрицательное число

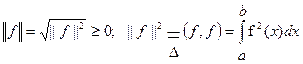 (3)
(3)
Свойства нормы 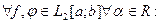
1) || f ||=0 ó f(x) ≡ 0; 2) || α∙f || = |α|∙ || f ||;
3) ||f ± φ|| ≤ ||f || + ||φ||
Определение 4. Функции 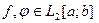 называются ортогональными, если (f,φ)=0.
называются ортогональными, если (f,φ)=0.
Множество F={φi(x), i=1,2,…} 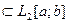 называется ортогональным, если его элементы – попарно ортогональные функции:
называется ортогональным, если его элементы – попарно ортогональные функции: 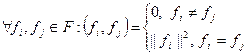
ЭКЗ. Доказать, что множество 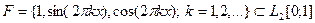 ортогонально на [0;1] и вычислить нормы этих функций.
ортогонально на [0;1] и вычислить нормы этих функций.
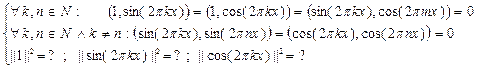
======================================
§2 Понятие о ряде Фурье. Коэффициенты Фурье. Многочлен наилучшего среднеквадратического приближения функции в L2([a;b]).
Пусть в L2([a;b]) задана бесконечная последовательность ортогональных функций
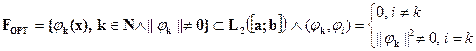
и задана функция g(x) 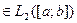 , так что для
, так что для 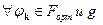 определены скалярные произведения и соответствующие нормы
определены скалярные произведения и соответствующие нормы 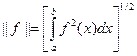 .
.
Определение 1. Числа 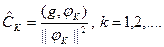 называются коэффициентами Фурье функции g по ортогональной системе FOPT, а функциональный ряд
называются коэффициентами Фурье функции g по ортогональной системе FOPT, а функциональный ряд 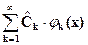 с этими коэффициентами – рядом Фурье.
с этими коэффициентами – рядом Фурье.
Рассмотрим множество «многочленовпорядка“n”»: 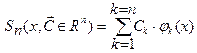 с произвольными коэффициентами
с произвольными коэффициентами 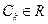 .
.
Теорема. Во множестве 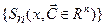 многочленов порядка n многочлен с коэффициентами Фурье
многочленов порядка n многочлен с коэффициентами Фурье
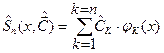 (3)
(3)
является многочленомнаилучшего среднеквадратического приближения функции g, минимизирующим норму разности 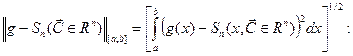
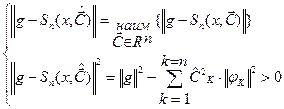 (4)
(4)
Доказательство.
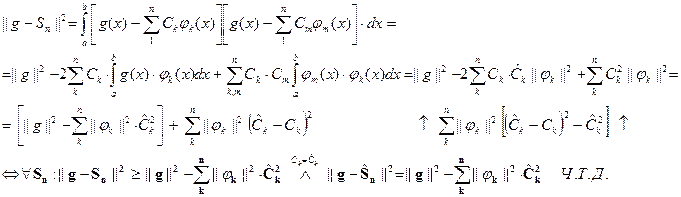
 2015-07-03
2015-07-03 242
242








