Тригонометрические ряды Фурье.
Определение.
Тригонометрическим рядом называется функциональный ряд вида
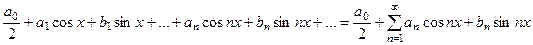 , (1)
, (1)
где 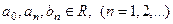 - коэффициенты ряда, которые вычисляются по формулам:
- коэффициенты ряда, которые вычисляются по формулам:
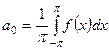 (2)
(2)
 (3)
(3)
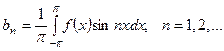 (4)
(4)
Для интегрируемой на отрезке 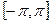 функции
функции 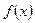 записывают
записывают
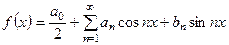
и говорят, что функции 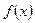 соответствует ее ряд Фурье. Если ряд Фурье сходиться, то его сумму обозначают
соответствует ее ряд Фурье. Если ряд Фурье сходиться, то его сумму обозначают 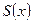 .
.
Теорема Дирихле
Пусть 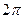 -периодическая функция
-периодическая функция 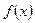 на отрезке
на отрезке 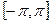 удовлетворяет условиям:
удовлетворяет условиям:
1. 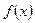 кусочно-непрерывна, т.е. непрерывна и имеет конечное число точек разрыва.
кусочно-непрерывна, т.е. непрерывна и имеет конечное число точек разрыва.
2. 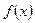 кусочно-монотонна, т.е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.
кусочно-монотонна, т.е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.
Тогда соответствующий функции 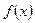 ряд Фурье сходится на этом отрезке и при этом:
ряд Фурье сходится на этом отрезке и при этом:
1. В точках непрерывности функции сумма ряда 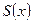 совпадает с самой функцией:
совпадает с самой функцией:
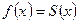 .
.
2. В каждой точке 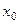 разрыва функции сумма ряда
разрыва функции сумма ряда
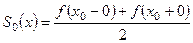 ,
,
т.е. равна среднему арифметическому пределов 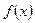 слева и справа.
слева и справа.
3. В точках 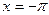 и
и 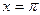 (на концах отрезка)
(на концах отрезка)
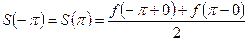 .
.
Таким образом, если 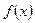 удовлетворяет условиям 1, 2 теоремы, то на отрезке
удовлетворяет условиям 1, 2 теоремы, то на отрезке 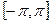 имеет место разложение
имеет место разложение
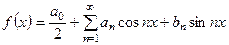 . (5)
. (5)
Это равенство может нарушаться только в точках разрыва функции 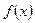 и на концах отрезка
и на концах отрезка 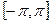 .
.
 2015-07-03
2015-07-03 8638
8638







