Разложение в ряд Фурье функции произвольного периода

Пусть функция 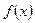, определенная на отрезке 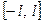, имеет период 2 l (f (x+ 2 l)= f (x), где l – произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле.

Сделаем подстановку 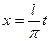, которая функцию 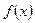преобразует в функцию 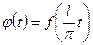, определенную на отрезке 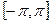и имеющую период .

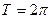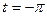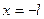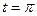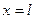Действительно, если , то , если , то и при 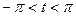имеем ;

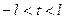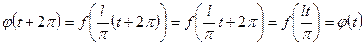, т.е. .

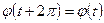Разложение функции 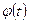в ряд Фурье на отрезке 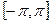имеет вид

,

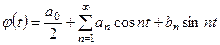где

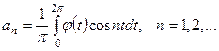
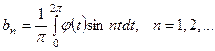
Возвращаясь к переменной x и заметив, что 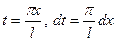, получим

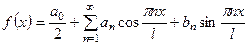, (10)

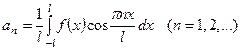, (11)

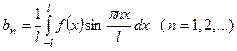. (12)

Замечание. Все теоремы, имеющие место для рядов Фурье 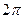- периодических функций, остаются в силе и для рядов Фурье функций с периодом .

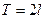Если f (x) – четная, то

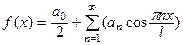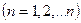, , (13)

где

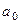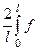= (x) dx; а_n = 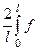(x) cos 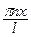dx, 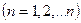. (14)

Если f (x) – нечетная, то

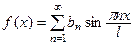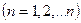, , (15)

где

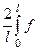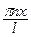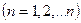b_n = (x) sin dx, . (16)