Решение

Функция f (x) имеет период 2 p. Она удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье.

f (– х) = – f (x) (рис. 3), т.е. f (x) – нечетна, следовательно 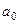= 0 и а_n = 0.

Рис. 3.

По формуле (9) найдем коэффициент Фурье:

b_n = 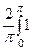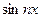dx = - 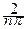cos nx 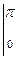= 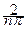(1–(–1) ⁿ ) =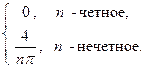

b _{2 k +1} = .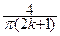

Следовательно, ряд Фурье для данной функции имеет вид:

f (x) = 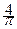(sin x + 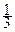sin x + 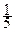sin x + … + 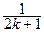sin((2 k +1)· x)), (k = 0,1,2,…)

f (x) = 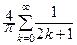sin ((2 k + 1) x).

При этом .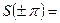

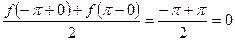На интервале 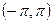ряд сходится к функции f (x), в точках х = 0 и х = ± p – к нулю.