Если функция 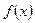 с периодом
с периодом 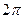 на отрезке
на отрезке 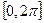 удовлетворяет условиям Дирихле, то для нее имеет место разложение (5), где коэффициенты вычисляются по формулам
удовлетворяет условиям Дирихле, то для нее имеет место разложение (5), где коэффициенты вычисляются по формулам
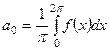
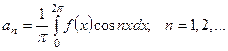
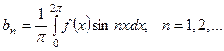
Пример 1: Разложить в ряд Фурье функцию с периодом 2p:
f (x) = 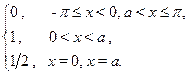
Решение:
Из определения f (x) следует, что она удовлетворяет условиям теоремы о разложимости в ряд Фурье, поэтому f (x) разлагается в ряд Фурье (см. рис. 1).
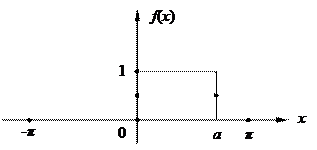 |
Рис. 1.
По формулам (2)-(4) находим коэффициенты Фурье:
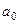 =
= 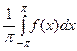 =
= 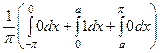 =
= 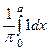 = а/p.
= а/p.
аn = 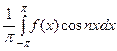 =
= 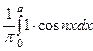 =
= 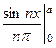 =
= 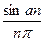 ,
,
bn = 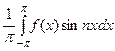 =
= 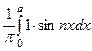 = –
= – 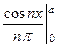 = –
= – 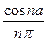 +
+ 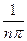 =
= 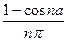 .
.
Следовательно,
f (x) = 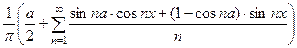 .
.
На интервале 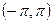 ряд сходится к функции f (x), в точках х = ± p к 0:
ряд сходится к функции f (x), в точках х = ± p к 0:
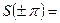
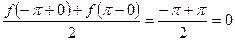 ,
,
в точках разрыва х = a, x = 0 к 1/2:
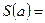
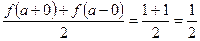 ,
,
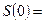
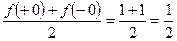 .
.
 2015-07-03
2015-07-03 1938
1938








