Предс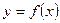тавление непериодической функции рядом Фурье

Пусть – непериодическая функция, заданная на всей оси .

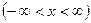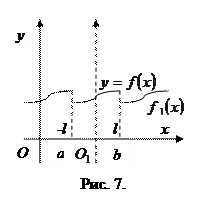Такая функция не может быть разложена в ряд Фурье, т.к. сумма ряда Фурье есть функция непериодическая и, следовательно, не может быть равна f (x) для всех x. В этом случае непериодическая функция f (x) может быть представлена в виде ряда Фурье на любом конечном промежутке 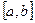, на котором она удовлетворяет условиям теоремы Дирихле. Для этого можно поместить начало координат в середину отрезка 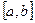и построить функцию 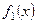с периодом 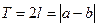такую, что 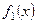= 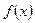при 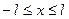(рис. 7).

Сумма этого ряда во всех точках отрезка 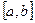(кроме точек разрыва) совпадает с заданной функцией 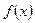. Вне этого промежутка сумма ряда и 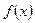являются совершенно различными функциями.

Пусть теперь непериодическую функцию 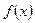требуется разложить в ряд Фурье на отрезке 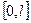. Такую функцию можно произвольным образом доопределить на отрезке 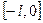нечетным или четным способом (сохраняя кусочную монотонность), а затем разложить в ряд Фурье по синусам или косинусам соответственно (рис. 8, 9).

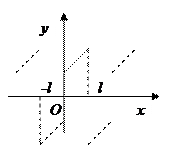
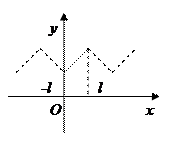
Рис.8.

Рис. 9.

Пример7. Функцию f (x) = 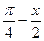разложить в ряд косинусов на интервале (0; p).