Произведением двух событий А и В называют событие C=АВ, состоящее в совместном появлении (совмещении) этих событий.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, событие АВС состоит в совмещении событий А, В и С.
Два события называют независимыми, если вероятность одного из них не зависит от появления или непоявления другого.
Теорема. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Р(АВ)=Р(А)× Р(В).
Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Р(А1 А2... Аn) = Р(А1) · Р(А2)...Р(Аn).
Пример 5. Найти вероятность совместного появления герба при одном бросании двух монет.
Решение. Обозначим события: А - появление герба на первой монете, В - появление герба на второй монете, С - появление герба на двух монетах С=АВ.
Вероятность появления герба первой монеты:
Р(А) = 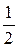 .
.
Вероятность появления герба второй монеты:
Р(В) = 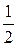 .
.
Так как события А и В независимые, то искомая вероятность по теореме умножения равна:
Р(С)=Р(АВ) = Р(А)×Р(В) = 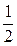 ×
× 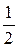 =
= 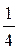 .
.
Пример 6. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика вынута стандартная деталь (событие А):
Р(А) = 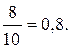
Вероятность того, что из второго ящика вынута стандартная деталь (событие В):
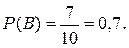
Вероятность того, что из третьего ящика вынута стандартная деталь (событие С):
Р(С)= 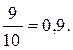
Так как события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения) paвна:
P(ABC)=P(A)×P(B)×P(C)= 0,8 0,7×0,9 = 0,504.
Пример 7. Вероятности появления каждого из двух независимых событий А1 и А2 соответственно равны р1 и р2. Найти вероятность появления только одного из этих событий.
Решение. Введем обозначения событий:
В1 – появилось только событие А1; В2 – появилось только событие А2.
Появление события В1 равносильно появлению события А1 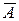 2 (появилось первое событие и не появилось второе), т.е. В1= А1
2 (появилось первое событие и не появилось второе), т.е. В1= А1 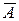 2.
2.
Появление события В2 равносильно появлению события 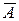 1А2 (не появилось первое событие и появилось второе), т.е. В1=
1А2 (не появилось первое событие и появилось второе), т.е. В1= 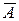 1А2.
1А2.
Таким образом, чтобы найти вероятность появления только одного из событий А1 или А2, достаточно найти вероятность появления одного, безразлично какого из событий В1 и В2. События В1 и В2 несовместны, поэтому применима теорема сложения несовместных событий:
Р(В1+В2) = Р(В1) + Р(В2).
Остается найти вероятности каждого из событий В1 и В2. События А1 и А2 независимы, следовательно, независимы и противоположные события, поэтому применима теорема умножения:
Р(В1) = Р(А1 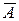 2)=Р(А1)×Р(
2)=Р(А1)×Р( 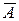 2)= р1q2,
2)= р1q2,
Р(В2) = Р( 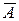 1А2)=Р(
1А2)=Р( 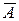 1)×Р(А2)= q1p2,
1)×Р(А2)= q1p2,
где q1 и q2 – вероятность событий 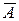 1 и
1 и 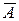 2 соответственно.
2 соответственно.
Найдем искомую вероятность появления только одного из событий А1 и А2:
Р(В1+В2) = Р(В1) + Р(В2) = р1q2 + q1p2.
Пример 8. Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй - 0,9, третий - 0,8.Найти вероятность того, что студент сдаст: а) только второй экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.
Решение. а) Введем обозначения событий:
А1 – студент сдаст первый экзамен, 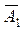 - не сдаст первый экзамен;
- не сдаст первый экзамен;
А2 – студент сдаст второй экзамен, 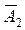 - не сдаст второй экзамен;
- не сдаст второй экзамен;
А3 – студент сдаст третий экзамен, 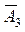 - не сдаст третий экзамен;
- не сдаст третий экзамен;
А – студент сдаст только второй экзамен из трех, то есть: 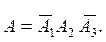
Так как события А1, А2 и А3 независимы, получим:
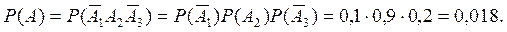
б) Обозначим события:
В - студент сдаст один экзамен из трех;
В1 – студент сдаст только первый экзамен А1: 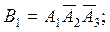
В2 – студент сдаст только второй экзамен А2: 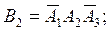
В3 – студент сдаст только третий экзамен А3: 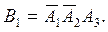
События В1, В2 и В3 несовместны, поэтому применима теорема сложения несовместных событий:
Р(В)=Р(В1)+Р(В2)+Р(В3)= 0,9×0,1×0,2+0,1×0,9×0,2+0,1×0,1×0,8=0,044.
в) Обозначим событие С - студент сдаст все три экзамена, т.е. С=А1А2А3. Тогда:
Р(С)=Р(А1А2А3)= Р(А1 )Р(А2)Р(А3)= 0,9×0,9×0,8=0,648.
г) Обозначим событие D - студент сдаст по крайней мере два экзамена (иначе говоря: хотя бы два экзамена или не менее двух экзаменов). Событие D означает, что студент сдаст или любые два экзамена из трех или все три экзамена, то есть:
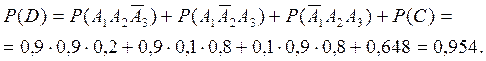
д) Обозначим события:
Е - студент сдаст хотя бы один экзамен;
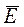 - студент не сдаст ни одного экзамена.
- студент не сдаст ни одного экзамена.
События Е и 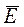 - противоположные, поэтому можно применить теорему сложения вероятностей противоположных событий:
- противоположные, поэтому можно применить теорему сложения вероятностей противоположных событий:
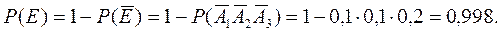
 2015-07-02
2015-07-02 5356
5356
