Комплексная форма ряда Фурье

Пусть f(x) удовлетворяет условиям Дирихле на [-l;l] и, следовательно, может быть разложена в ряд Фурье:

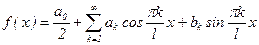, где

, , .

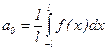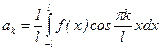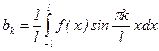Используя формулы Эйлера 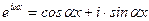, 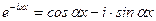или 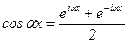; 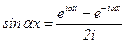, представим одну гармонику 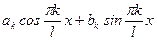в другом виде:

= =

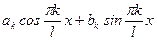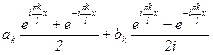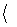во втором слагаемом избавимся от мнимой единицы в знаменателе, домножив и числитель, и знаменатель дроби на " i "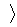

= = = ;

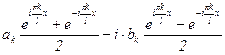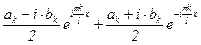обозначим 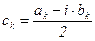; 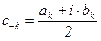. Учитывая формулы для a_k и b_k, имеем: ;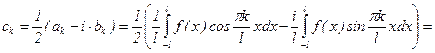

.

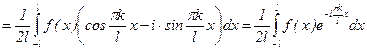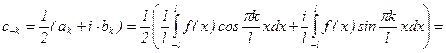
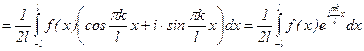Последние равенства в выражениях для c_k и c_-k получены с учетом формул Эйлера. Учитывая, что 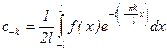, можно записать c_k и c_-k одним выражением: 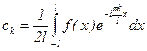, k=0,±1, ±2,... Заметим, что .

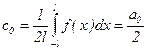Используя новое выражение для гармоники, частичную сумму ряда Фурье для f(x) можно записать в виде:

;

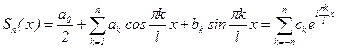а сам ряд Фурье, порождаемый f(x) имеет вид: 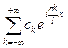. Он сходится к f(x), если существует 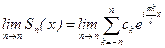. Так определенная сходимость называется сходимостью в смысле главного значения.

Итак, имеет место равенство:

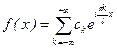, где .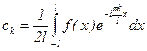

Это равенство и есть разложение f(x) в ряд Фурье в комплексной форме.