При решении задач о разложении функции f(x) в ряд Фурье следует:
1) нарисовать график f(x) на промежутке хотя бы длиной в два периода, чтобы показать, что данная функция периодическая;
2) нарисовать график S(x) аналогично, чтобы было видно в каких точках f(x)¹S(x);
3) вычислить коэффициенты Фурье и записать ряд Фурье.
Задачи
№1. Разложить в ряд Фурье 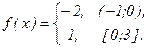
Решение. Заметим, что f(x) задана на промежутке длины T = 4. Т.к. f(x) предполагается периодической, то именно это число и является ее периодом, тогда l = 2.
1) График f(x):
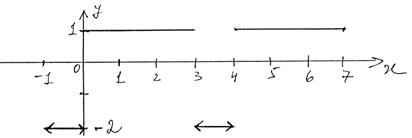
\
2) График S(x):
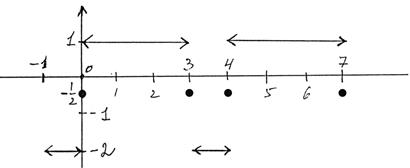
Стрелки в концах линий показывают, что функция не принимает в концах интервала значения, определяемого из выражения, заданного на интервале. При сравнении графиков f(x) и S(x) хорошо видно, что в точках разрыва f(x)¹S(x).
3) Вычислим коэффициенты Фурье. Это можно сделать по формулам (3*): 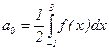 ;
; 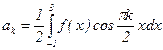 ;
; 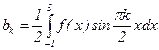 . Именно:
. Именно: 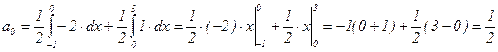 ; итак,
; итак,
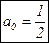 .
.
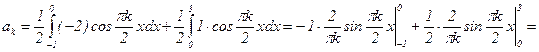
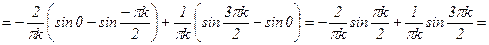
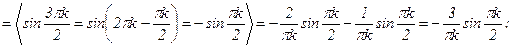
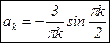
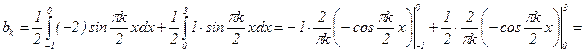
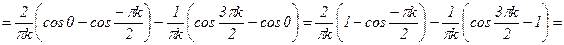
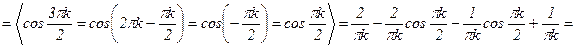
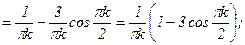
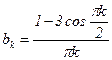
Разложение f(x) в ряд Фурье имеет вид:
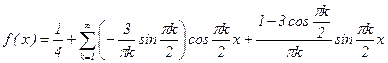
Замечания. 1) При интегрировании на [-1;3] этот отрезок был разбит на [1;0] и [0;3], т.к. на этих отрезках f(x) задана разными значениями.
2) При вычислении коэффициентов использованы интегралы: 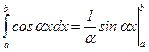 и
и 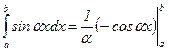 , где a = const.
, где a = const.
№2. Разложить в ряд Фурье 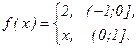
Решение. Здесь T = 2, l = 1.
Ряд Фурье имеет вид: 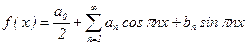 , где
, где 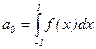 ;
; 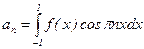 ;
; 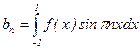 , т.к. l = 1.
, т.к. l = 1.
1) 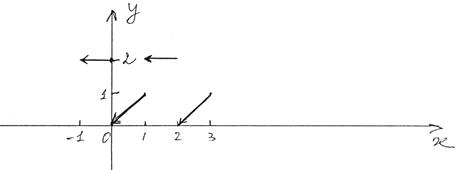 График f(x):
График f(x):
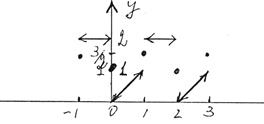
2) График S(x):
3) 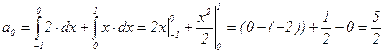 ;
; 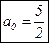 .
.
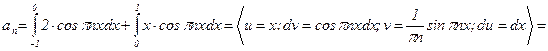
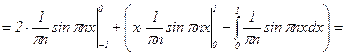
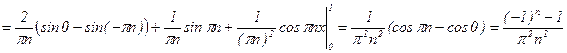 ;
; 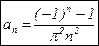 ;
; 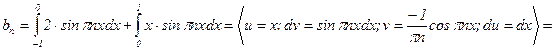
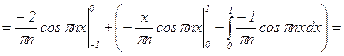
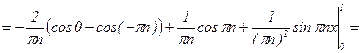
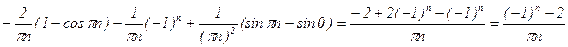 ;
; 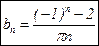
Тогда 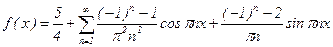
№3. Разложить в ряд Фурье по синусам 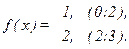
Решение. Заметим, что в ряд Фурье по синусам раскладываются только нечетные функции. Т.к. f(x) определена только для x > 0, xÎ(0;2)È(2;3), то это означает, что на симметричный промежуток (-3;-2)È(-2;0) f(x) нужно продолжить так, чтобы выполнялось равенство f(-x) = -f(x). Поэтому длина промежутка, на котором f(x) задана как нечетная функция, равна 6. Значит T = 6, l = 3. Ряд Фурье для f(x) имеет вид: 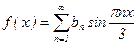 , где
, где 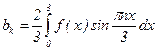 , n = 1, 2, 3, (по формулам (5')).
, n = 1, 2, 3, (по формулам (5')).
1) График f(x).
Чтобы нарисовать график f(x) как нечетной функции, нарисуем сначала график на (0;2)È(2;3), а затем воспользуемся тем, что график нечетной функции симметричен относительно начала координат. Из этих соображений получаем график f(x) на (-3;-2)È(-2;0). Затем продолжаем f(x) на всю числовую прямую как периодическую функцию с периодом T = 6.
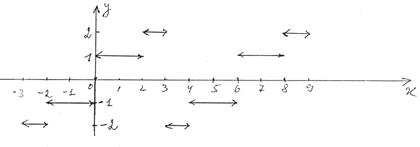
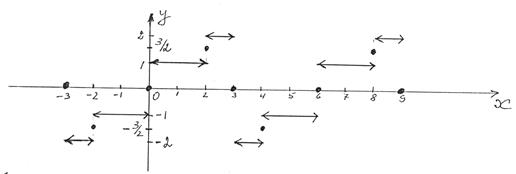
2) График S(x).
График S(x) отличается от графика f(x) в точках разрыва функции f(x). Например, в т. x = 2 f(x) не определена, а S(x) имеет при x = 2 значение, равное полусумме односторонних пределов функции f(x), именно: 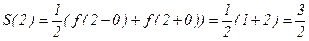 , где
, где 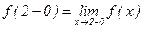 ,
, 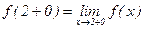 .
.
3) 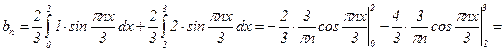
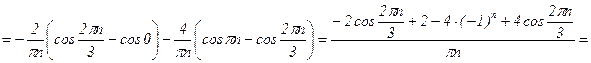
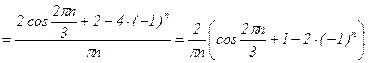 .
.
Итак, 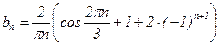 , тогда разложение f(x) в ряд Фурье имеет вид:
, тогда разложение f(x) в ряд Фурье имеет вид: 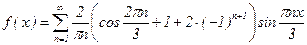 .
.
№4. Разложить в ряд Фурье по косинусам 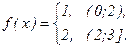 .
.
Решение. Заметим, что в ряд Фурье по косинусам раскладываются только четные функции. Т.к. f(x) задана только для x>0, xÎ(0;2)È(2;3], то это означает, что на симметричный промежуток [-3;-2)È(-2;0) f(x) нужно продолжить так, чтобы выполнялось равенство: f(-x) = f(x). Поэтому длина промежутка, на котором f(x) задана как четная функция, равна 6, тогда T = 6, l = 3. Ряд Фурье в этом случае имеет вид:
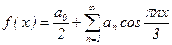 ,
,
где 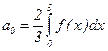 ;
; 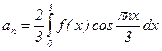 ; n = 1,2,... (по формулам (4')).
; n = 1,2,... (по формулам (4')).
1) График f(x).
Чтобы нарисовать график f(x) как четной функции, нарисуем сначала график f(x) на (0;2)È(2;3], а затем воспользуемся тем, что график четной функции симметричен относительно оси ординат. Из этих соображений получаем график f(x) на [-3;-2)È(-2;0). Затем продолжаем f(x) на всю числовую прямую как периодическую функцию с периодом T = 6.
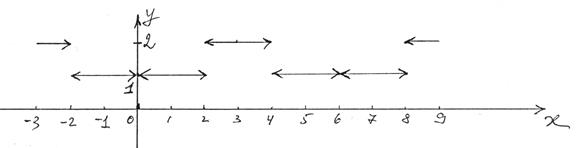
Здесь график f(x) нарисован на двух полных периодах функции.
2) График S(x).
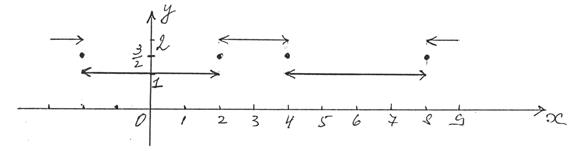
График S(x) отличается от графика f(x) в точках разрыва функции f(x). Например, в т. x = 0 f(x) не определена, а S(x) имеет значение: 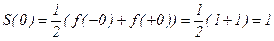 , поэтому график S(x) не прерывается в т. x = 0, в отличие от графика f(x).
, поэтому график S(x) не прерывается в т. x = 0, в отличие от графика f(x).
3) 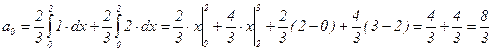 ;
; 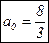 .
.
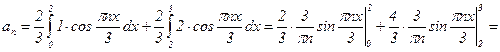
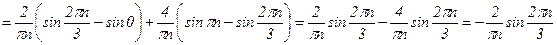 ;
; 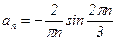
Разложение f(x) в ряд Фурье по косинусам имеет вид: 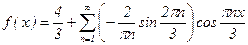 .
.
№5. Разложить в ряд Фурье f(x) = |x|, xÎ(-2;2)..
Решение. По условию, f(x) является четной функцией на (-2;2); т.е. ее ряд Фурье содержит только косинусы, при этом T = 4, l = 2, 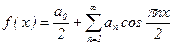 ,
,
где 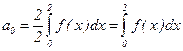 ;
; 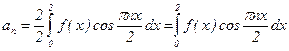 ; n = 1, 2,
; n = 1, 2,
1) График f(x):
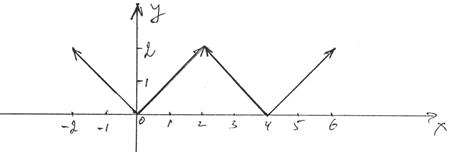
2) График S(x):
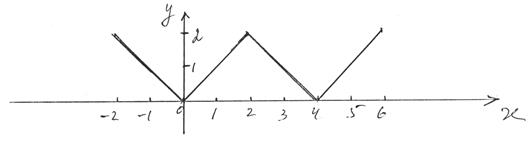
3) 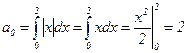 , т.к. |x| = x для x > 0.
, т.к. |x| = x для x > 0. 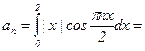
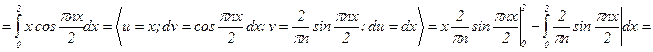
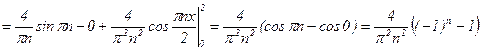 ;
; 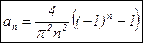 .
.
Тогда разложение f(x) в ряд Фурье имеет вид: 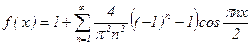 . Заметим, что при интегрировании выражений
. Заметим, что при интегрировании выражений 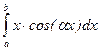 или
или 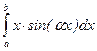 применяется формула интегрирования по частям:
применяется формула интегрирования по частям: 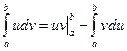 , где u = x; dv = cos(ax)dx или dv = sin(ax)dx.
, где u = x; dv = cos(ax)dx или dv = sin(ax)dx.
№6. Разложить функцию 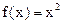 в ряд Фурье: а) в интервале (–?,?); б) в интервале (0, 2?); в) в интервале (0,?) в ряд синусов.
в ряд Фурье: а) в интервале (–?,?); б) в интервале (0, 2?); в) в интервале (0,?) в ряд синусов.
Решение. а) График функции с 2? - периодическим продолжением имеет вид
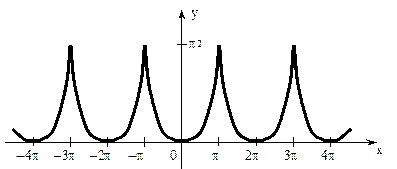
Функция удовлетворяет условиям теоремы Дирихле и потому ее можно разложить в ряд Фурье.
Вычислим коэффициенты Фурье. Так как функция четная, то bn = 0 (n = 0, 1, 2,…) и (n = 0, 1, 2,…). 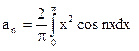
Для вычисления этого интеграла применяют формулу интегрирования по частям в определенном интеграле. Получаем
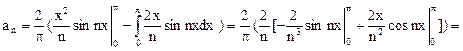
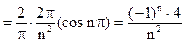
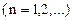
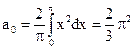 .
.
Ряд Фурье данной функции имеет вид 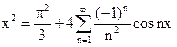 . В силу признака Дирихле данный ряд представляет функцию х2 в интервале (–?,?).
. В силу признака Дирихле данный ряд представляет функцию х2 в интервале (–?,?).
б) Интервал (0, 2?) не симметричен относительно начала координат, а длина его 2 l = 2?. Вычисляем коэффициенты Фурье по формулам:
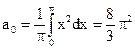 ,
,
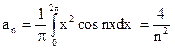
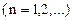
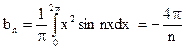 .
. 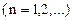
Поэтому ряд Фурье имеет вид 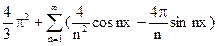 . В силу теоремы Дирихле ряд сходится к порождающей функции в точках х?(0,2?), а в точках 0 и 2? к значению. График суммы ряда имеет вид
. В силу теоремы Дирихле ряд сходится к порождающей функции в точках х?(0,2?), а в точках 0 и 2? к значению. График суммы ряда имеет вид 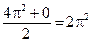
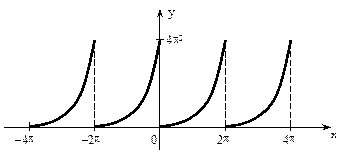
в) Функция, разлагаемая в ряд по синусам, должна быть нечетной. Следовательно, доопределим заданную функцию х2 в (–π,π) нечетным образом, т.е. рассматриваем функцию 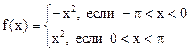 . Для этой функции f(x) имеем аn = 0 (n = 0, 1, 2,…) и
. Для этой функции f(x) имеем аn = 0 (n = 0, 1, 2,…) и 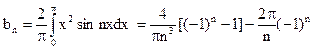
Искомое разложение имеет вид 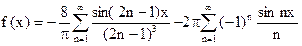 .
.
График суммы ряда имеет вид
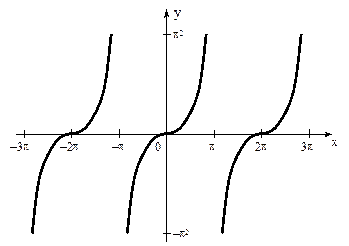
Отметим, что в точках х = (–π,π) ряд Фурье сходится к нулю.
№7 Разложить в ряд Фурье функцию, заданную графически:
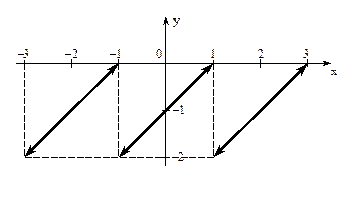
Решение. Получим явное выражение для f(x). График функции – прямая линия, используем уравнение прямой в виде 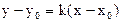 . Как видно из чертежа,
. Как видно из чертежа, 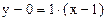 , т.е. f(x) = x – 1 (–1 < x < 1) и период Т = 2.
, т.е. f(x) = x – 1 (–1 < x < 1) и период Т = 2.
Эта функция удовлетворяет условиям признака Дирихле, поэтому она разлагается в ряд Фурье. Вычислим коэффициенты Фурье (l = 1):
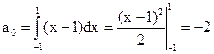
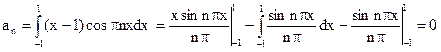 ; (n = 1, 2,…);
; (n = 1, 2,…);
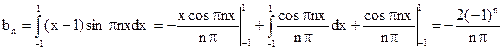 .
.
Ряд Фурье для функции f(x) имеет вид
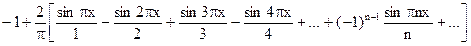 .
.
Он представляет функцию f(x) при –1 < x < 1, а в точках х0 = –1 и х0 = 1 ряд сходится к –1.
№8. Разложить функцию 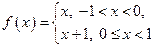 в тригонометрический ряд Фурье на отрезке и указать функцию, к которой сходится полученный ряд.
в тригонометрический ряд Фурье на отрезке и указать функцию, к которой сходится полученный ряд.
Решение. Нарисовать график функции, продолжив ее периодически с периодом 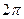 или
или 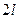 на всю ось. Продолженная функция имеет период
на всю ось. Продолженная функция имеет период 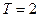 .
.
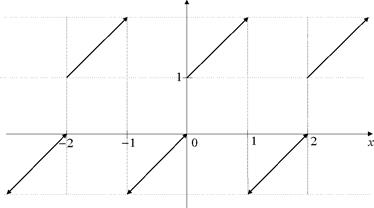
Проверить условия достаточных признаков сходимости ряда Фурье (Дини-Липшица, Жордана, Дирихле).
Функция 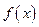 кусочно-монотонна на отрезке
кусочно-монотонна на отрезке 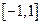 : она возрастает на
: она возрастает на 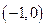 и на
и на 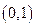 . В точках
. В точках 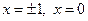 функция имеет разрывы первого рода.
функция имеет разрывы первого рода.
Выяснить четность или нечетность функции: Функция не является ни четной, ни нечетной.
Вычислить коэффициенты Фурье по формулам:
а) если функция задана на 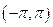
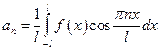

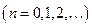 ,
,
б) если функция задана на 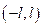
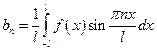
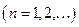 .
.
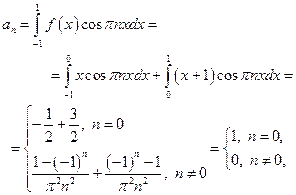
Составить ряд Фурье функции 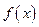 :
: 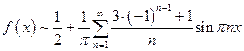 .
.
Указать функцию, к которой будет сходиться этот ряд, пользуясь поточечными признаками сходимости: Согласно признаку Дирихле ряд Фурье функции 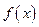 сходится к сумме:
сходится к сумме:
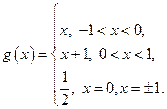
№9. Разложить функцию 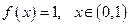 , в ряд Фурье по синусам на
, в ряд Фурье по синусам на 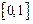 и с помощью этого разложения найти сумму числового ряда
и с помощью этого разложения найти сумму числового ряда 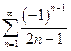 .
.
Решение. Продолжить функцию четным (нечетным) образом на (– p,0) или (– l,0), а затем периодически с периодом 2 p или 2 l продолжить функцию на всю ось.
Продолжим функцию нечетным образом на 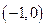 , а затем периодически, с периодом
, а затем периодически, с периодом 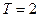 , продолжим ее на всю ось.
, продолжим ее на всю ось.
Нарисовать график периодического продолжения. Мы получим функцию  вида:
вида:
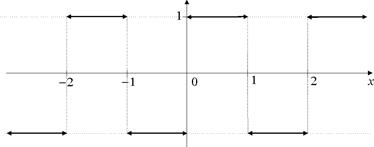
Проверить условия достаточных признаков сходимости ряда Фурье (Дини-Липица, Жордана, Дирихле).
Функция  кусочно-постоянна в промежутке
кусочно-постоянна в промежутке 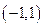 : она равна –1 на
: она равна –1 на 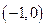 и 1 на
и 1 на 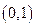 . В точках
. В точках 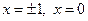 функция имеет разрывы первого рода.
функция имеет разрывы первого рода.
Вычислить коэффициенты Фурье:
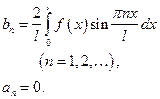
Ее коэффициенты Фурье вычисляются по формулам:
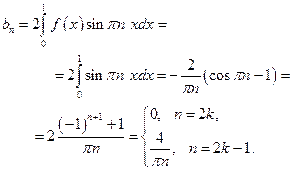
Составить ряд Фурье функции 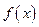 .
. 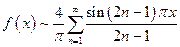 .
.
Указать функцию, к которой будет сходиться этот ряд, пользуясь поточечными признаками сходимости.
Согласно признаку Дирихле ряд Фурье функции 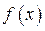 сходится к сумме:
сходится к сумме:
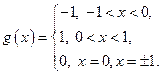
Следовательно, при 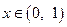
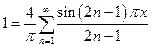
Подставив значения 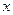 , указать сумму заданного числового ряда.
, указать сумму заданного числового ряда.
Полагая в полученном разложении 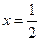 , найдем
, найдем 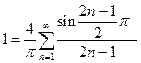 ,
,
откуда, так как 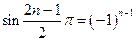 ,
, 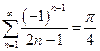 .
.
№10. Написать равенство Парсеваля для функции 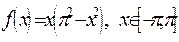 , и, исходя из этого равенства, найти сумму числового ряда
, и, исходя из этого равенства, найти сумму числового ряда 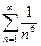 .
.
Решение. Установить, является ли данная функция функцией с интегрируемым квадратом на 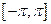 .
.
Функция 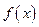 непрерывна, а, следовательно, интегрируема на
непрерывна, а, следовательно, интегрируема на 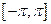 . По той же причине ее квадрат интегрируем на
. По той же причине ее квадрат интегрируем на 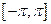 .
.
Вычислить коэффициенты Фурье по формулам:
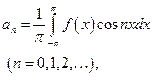
Так как 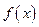 нечетная функция, то ее коэффициенты Фурье вычисляются по формулам:
нечетная функция, то ее коэффициенты Фурье вычисляются по формулам: 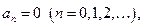
Вычислить интеграл 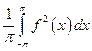 .
.
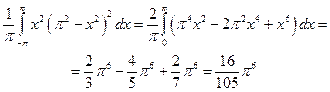
Написать формулу Парсеваля: 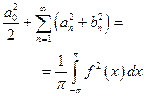
Таким образом, формула Парсеваля имеет вид 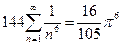
Произведя, если требуется, арифметические действия в правой и левой частях, получить сумму данного числового ряда.
Разделив обе части полученного равенства на 144, найдем:  .
.
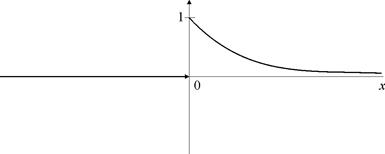
№11. Найти интеграл Фурье функции 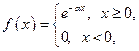
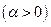
и построить его график.
Решение. Построить график функции 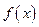 .
.
Проверить выполнение условий достаточных признаков сходимости интеграла Фурье (Дини, Дирихле-Жордана или следствий из них).
Функция 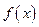 абсолютно интегрируема в промежутке
абсолютно интегрируема в промежутке 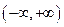 , непрерывна при
, непрерывна при 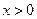 и
и 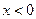 , а в точке
, а в точке 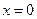 имеет разрыв первого рода. Далее, при
имеет разрыв первого рода. Далее, при 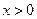 и
и 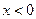 функция
функция 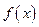 имеет конечную производную, а в нуле существуют конечные правая и левая производные. Выяснить четность или нечетность функции. Функция
имеет конечную производную, а в нуле существуют конечные правая и левая производные. Выяснить четность или нечетность функции. Функция 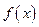 не является ни четной, ни нечетной.
не является ни четной, ни нечетной.
Вычислить коэффициенты по формулам:
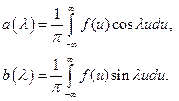 Имеем:
Имеем: 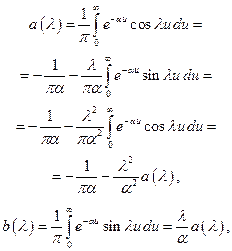
откуда 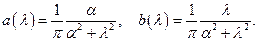
Записать интеграл Фурье функции 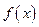 :
:
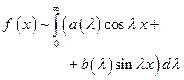
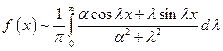
Указать функцию, к которой будет сходиться интеграл Фурье, пользуясь поточечными признаками сходимости.
Согласно следствию из признака Дини интеграл Фурье функции 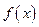 сходится всюду к функции
сходится всюду к функции
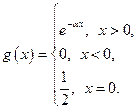
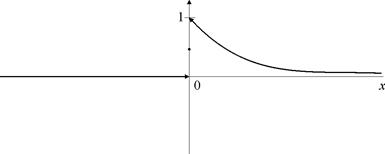
Построить график полученной функции
№12. Найти синус-преобразование Фурье функции 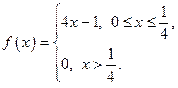
Решение. Проверить, будет ли заданная функция абсолютно интегрируемой на всей оси (в случае косинус- или синус-преобразования – на полупрямой 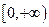 ).
).
Функция 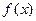 абсолютно интегрируема на полупрямой
абсолютно интегрируема на полупрямой 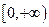 , что следует из ее непрерывности на этом промежутке
, что следует из ее непрерывности на этом промежутке
Вычислить преобразование Фурье по формуле:
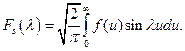
Ее синус-преобразование Фурье есть 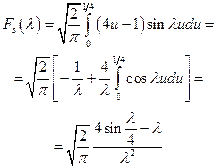
№13. Разложить в ряд Фурье периодическую функцию 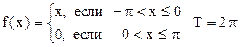 .
.
Решение. Сделать чертеж, при этом если функция задана лишь на периоде [например, на (–p,p)], продолжить ее периодически на всю числовую прямую
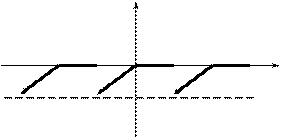 Y
Y
-2π -π 0 π 2π 3π x
Проверить условие теоремы Дирихле для данной функции:
а) ограничена;
б) кусочно-монотонна;
а) 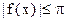 ;
;
б) на (0, p) – постоянна, на (–p, 0) – возрастает;
Выяснить четность и нечетность функции
Вычислить коэффициент Фурье по формулам:
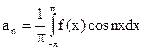 (n = 0, 1, …);
(n = 0, 1, …);
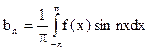 (n = 1, 2, …).
(n = 1, 2, …).
Для четных функций 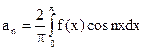 (n = 0, 1,);
(n = 0, 1,);
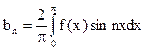 (n = 1,2,…).
(n = 1,2,…).
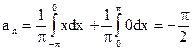 ;
;
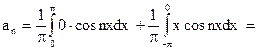
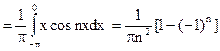 ;
;
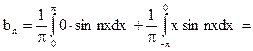
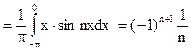 .
.
Составить ряд Фурье функции f(x), при этом в случае четной функции он должен содержать лишь косинусы, а для нечетной функции – лишь синусы
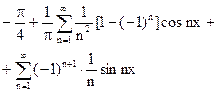
Сделать вывод о сходимости полученного ряда Фурье, используя правило: сумма ряда равна:
а) f(x) в тех внутренних точках интервала (-p, p), в которых функция непрерывна;
б) 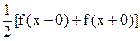 во всех точках разрыва функции f(x);
во всех точках разрыва функции f(x);
в) 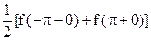 на концах интервала
на концах интервала
Ряд сходится к f(x) при х Î (-p, p), в точках ±p сходится к 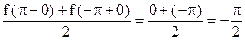
№14. Представить рядом Фурье в комплексной форме
f(x) = ex, o£ x< 2p; T = 2p.
Решение. Здесь T = 2p Þ l = p и ряд Фурье имеет вид: 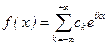 , где
, где 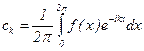 .
.
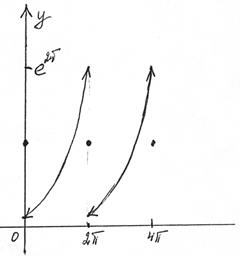
1) График f(x):
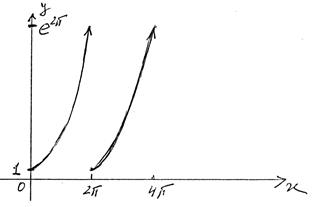
2) График S(x):
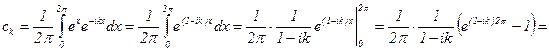

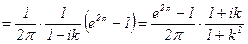 . Итак,
. Итак, 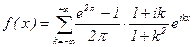 , или
, или 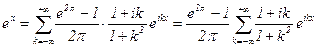 , xÎ[0;2p).
, xÎ[0;2p).
Заметим, что при вычислении ck использовано свойство: 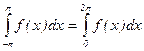 , если f(x) – периодическая функция с периодом T = 2p.
, если f(x) – периодическая функция с периодом T = 2p.
№ 15. Представить рядом Фурье в комплексной форме f(x) = 2x, xÎ(-1;1), T = 2.
Решение. Здесь T = 2, l = 1 и ряд Фурье имеет вид: 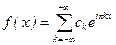 , где
, где 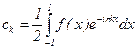 .
.
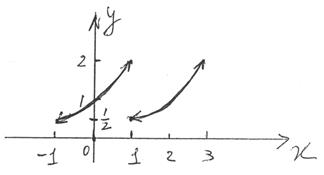 1) График f(x):
1) График f(x):
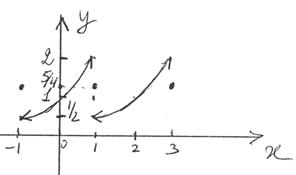
2) График S(x):
3) 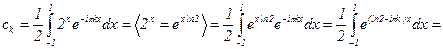
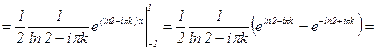
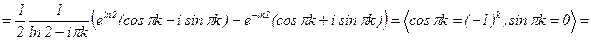
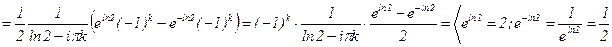 ;
; 
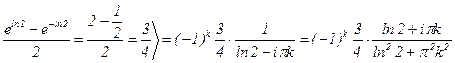 .
.
Итак, 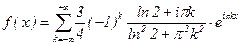 , или
, или 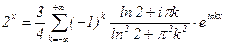 ,
,
xÎ(-1;1).
 2015-07-03
2015-07-03 42182
42182
