Перечень основных умений

Разложение в ряд Фурье периодической функции, заданной на (-p, p) или (-l, l)

1. Сделать чертеж, при этом, если функция задана на периоде [например, (-p,p)], продолжить ее периодически на всю числовую ось.

2. Проверить условия теоремы Дирихле для данной функции:

а) ограничена;

б) кусочно-монотонна.

3. Выяснить четность и нечетность функции.

4. Вычислить коэффициенты Фурье по правилам:

а) если функция задана на (-p, p), то

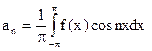(n = 0, 1, …); 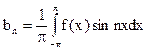(n = 1, 2, …);

б) если функция задана на (- l, l), то

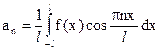(n = 0, 1, …);

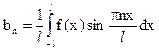(n = 1, 2, …).

Если функция f(x) четная, то

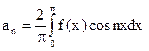(n = 0, 1, 2,…), b_n=0

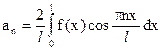(n = 0, 1,…), b_n=0

Если функция f(x) нечетная, то

а_n = 0 (n = 0,1,…), 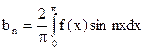(n = 1, 2, …)

а_n = 0 (n = 0,1,…), 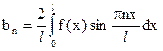(n = 1, 2, …).

5. Составить ряд Фурье функции f(x), при этом в случае четной функции он должен содержать лишь косинусы, а для нечетной функции – лишь синусы.

6. Сделать вывод о сходимости полученного ряда Фурье, используя правило: сумма ряда равна:

а) 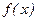в тех внутренних точках интервала (-p, p) [или (- l, l)], в которых функция непрерывна;

б) 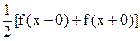во всех точках разрыва функции f(x);

в)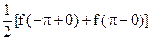

(или 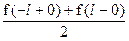) на концах интервала.

ЛИТЕРАТУРА