Неполные ряды Фурье

Пусть f(x) – на [-l;l] удовлетворяет условиям Дирихле. Особый интерес представляют два случая.

1) Для f(x) на [-l;l] выполняется равенство f(-x)=f(x), т.е. f(x) является четной функцией. Тогда 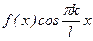, k=1,2,... – также четная функция, а 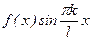– нечетная. Отсюда

-

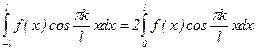как интеграл от четной функции по симметричному промежутку, а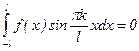

как интеграл от нечетной функции по симметричному промежутку. Поэтому ряд Фурье имеет вид:

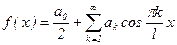, (4)

где 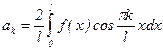; ; 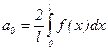b_k=0. (4')

2) Для f(x) на [-l;l] выполняется равенство f(-x)=-f(x), т.е. f(x) является нечетной функцией. Тогда 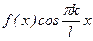, k=1,2,... – также нечетная функция, а 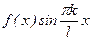– четная. Отсюда 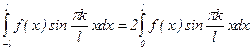как интеграл от четной функции по симметричному промежутку, а 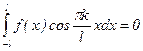как интеграл от нечетной функции по симметричному промежутку. Поэтому ряд Фурье имеет вид:

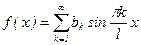, (5)

Где 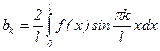, a₀=0, a_k=0. (5')

Нетрудно заметить, что ряд Фурье для четной функции содержит только косинусы, а ряд Фурье для нечетной функции – только синусы. Поэтому задача о разложении такой функции в ряд Фурье часто формулируется как задача о разложении по косинусам или по синусам соответственно.