Рассмотрим тригонометрический ряд (1). Для изучения его сходимости естественно рассмотреть числовой ряд
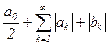 , (2)
, (2)
который мажорирует ряд (1), т.к. a0£|a0|, 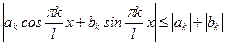 . Тогда если ряд (2) сходится, то ряд (1) сходится при всех x абсолютно и равномерно (по признаку Вейерштрасса). Но ряд (1) может сходиться и при отсутствии сходимости ряда (2). Рассмотрим соответствующие признаки сходимости подобных рядов.
. Тогда если ряд (2) сходится, то ряд (1) сходится при всех x абсолютно и равномерно (по признаку Вейерштрасса). Но ряд (1) может сходиться и при отсутствии сходимости ряда (2). Рассмотрим соответствующие признаки сходимости подобных рядов.
Теорема 1. Если f(x) с периодом 2l непрерывна для всех xÎR и имеет кусочно-непрерывную производную на периоде 2l, то её ряд Фурье равномерно сходится к ней для xÎR.
Определение. Говорят, что f(x) периода 2l удовлетворяет условиям Дирихле, если на [0;2l] можно указать конечное число точек 0=x0<x1<x2<...<xi<...<xN=2l таких, что для xÎ(xi,xi+1) f(x) ограничена, непрерывна и монотонна, а в любой точке xi разрыва имеет место равенство:
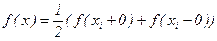 , (*)
, (*)
т.е. значение функции в этой точке равно полусумме односторонних пределов.
Теорема 2. (признак Дирихле). Если f(x) периода 2l удовлетворяет условиям Дирихле, то её ряд Фурье сходится к ней для любого xÎR.
Замечание. Если f(x) удовлетворяет условиям Дирихле, кроме условия (*), то ряд Фурье сходится к f(x) для всех xÎR, за исключением точек разрыва xi.
Если установлено, что ряд (1) равномерно сходится, то:
1) т.к. его элементы – непрерывные функции периода 2l, то его сумма f(x) есть непрерывная функция периода 2l;
2) ряд (1) можно почленно интегрировать, при этом имеет место равенство: 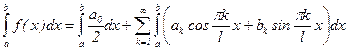 ;
;
3) ряд (1) можно формально продифференцировать: 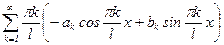 . Если этот ряд сходится равномерно, то
. Если этот ряд сходится равномерно, то 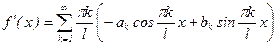 .
.
Вышеуказанные свойства выполняются на основании теории равномерно сходящихся рядов.
 2015-07-03
2015-07-03 3488
3488








