2015-07-03
1411
Рассмотрим систему функций с общим периодом 2l: 1,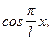 
,…, 
, 
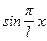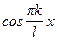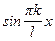,... Для них справедливы следующие соотношения:
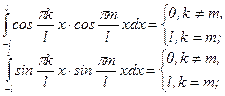
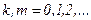
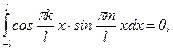
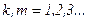
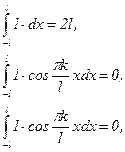
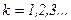
В этом случае говорят, что система функций на [-l;l] обладает свойством ортогональности. Покажем справедливость одного из этих равенств, например:
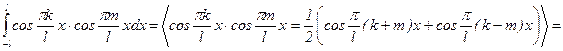
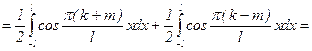
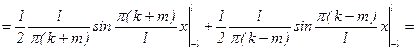
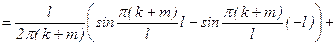
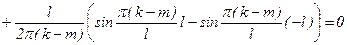, т.к. sin p(k+m)=0, sin p(k-m)=0.
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ ФУРЬЕ (ak,bk)
Изучение свойств функции f(x) в связи со сходимостью ряда (1) обусловлено тем, что коэффициенты Фурье определяются значениями этой функции. Покажем это.
Предположим, что ряд (1) сходится равномерно. Тогда его можно почленно интегрировать: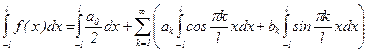 
. При этом, в силу ортогональности рассматриваемой системы функций, 
, 
, 
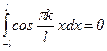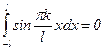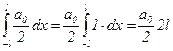. Тогда
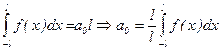. (3)
Умножим теперь ряд (1) почленно на функцию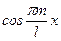 
. Т.к. 
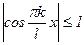, то равномерная сходимость ряда (1) сохранится. Проинтегрируем теперь результат умножения: 
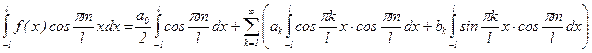, m=1,2,3... При этом, в силу ортогональности,
, 
,
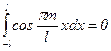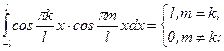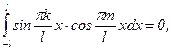
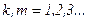
Тогда: m=k,
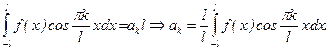(3')
Умножая почленно ряд (1) на функцию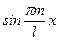 
и используя ортогональность рассматриваемой системы функций, аналогично получим:
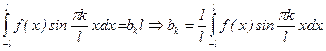(3")
Таким образом, показано, что коэффициенты Фурье определяются значениями функции f(x).
|
|
|
Замечания.
1) Можно показать, что формулы для ak,bk справедливы и в том случае, когда f(x) удовлетворяет условиям Дирихле;
2) Ввиду периодичности подынтегральных функций (T=2l), коэффициенты ak,bk можно вычислять, интегрируя по любому промежутку длиною в период, т.е.
; 
; 
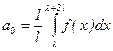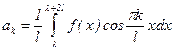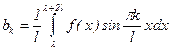, lÎR. (3*)
Рассматривая вновь сходящийся ряд (1), можно сказать, что f(x) разложена в ряд Фурье, коэффициенты которого вычисляются по формулам (3), (3'), (3"). Будем называть правую часть этого равенства суммой ряда Фурье и обозначать S(x). Ясно, что S(x)=f(x) в точках непрерывности f(x). Если xi – точка разрыва для f(x), то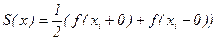 
, тогда как сама функция f(x) может быть не определена в точке разрыва xi или имеет там значение, отличное от полусуммы односторонних пределов. В этом случае равенство между S(x) и f(x) не выполняется.
