Дифференцирующие цифровые фильтры

Передаточная функция. Из выражения для производной d(exp(jwt))/dt = jw exp(jwt)

следует, что при расчете фильтра производной массива данных необходимо аппроксимировать рядом Фурье передаточную функцию вида H(w) = jw. Поскольку коэффициенты такого фильтра будут обладать нечетной симметрией (h_-n = -h_n) и выполняется равенство

h_n [exp(jwn)-exp(-jwn)] = 2j h_n sin nw,

то передаточная характеристика фильтра имеет вид:

H(w) = 2j(h₁ sin w + h₂ sin 2w +... + h_N sin Nw),

т.е. является мнимой нечетной, a сам фильтр является линейной комбинацией разностей симметрично расположенных относительно s_k значений функции. Уравнение фильтрации:

y_n = 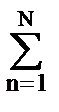h_n(s_k+n - s_k-n).

Если дифференцированию подлежит низкочастотный сигнал, а высокие частоты в массиве данных представлены помехами, то для аппроксимации в пределах главного частотного диапазона задается (без индекса мнимости) передаточная функция фильтра вида:

H(w) = w, w £ w_в, H(w) = 0, w_в< w £ w_N.

Оператор дифференцирующего фильтра:

h(n) = (2/p) 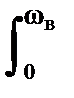H(w) sin(npw/w_N) dw, n = 0,1,2,... (7.5.1)

Принимая, как обычно, w_N = p (Dt = 1) и решая (7.5.1) при H(w) = w, получаем:

h_n = (2/p)[sin(nw_в)/n² - w_в cos(nw_в)/n], (7.5.2)

h_о = 0, h_-n = -h_n.

Частотная характеристика:

Im(H(w)) = 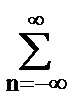h_n sin nw = 2 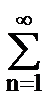h_n sin nw. (7.5.3)

Точность дифференцирования. На рис. 7.5.1 приведен пример расчета коэффициентов дифференцирующего фильтра на интервал частот {0-0.5}p при Dt=1 (w_в = p/2). Операторы дифференцирующих фильтров, как правило, затухают очень медленно и, соответственно, достаточно точная реализация функции (7.5.3) весьма затруднительна.

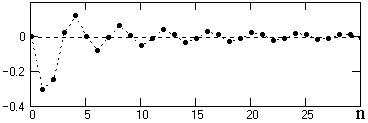Рис. 7.5.1. Коэффициенты оператора фильтра.

Ряд (7.5.3) усекается до N членов, и с помощью весовых функций производится нейтрализация явления Гиббса. Явление Гиббса для дифференцирующих фильтров имеет весьма существенное значение, и может приводить к большим погрешностям при обработке информации, если не произвести его нейтрализацию. Примеры ограничения оператора, приведенного на рис. 7.5.1, и соответствующие передаточные функции H'(w) усеченных операторов показаны на рис. 7.5.2.

Для оценки возможных погрешностей дифференцирования усеченными операторами произведем расчет фильтра при w_в = p/2. По формулам (7.5.2) определяем:

h_0-10 = 0, 0.3183, 0.25, -0.0354, -0.125, 0.0127, 0.0833, -0.0065, -0.0625, 0.0039, 0.05.

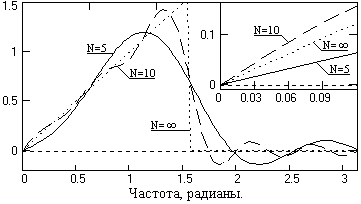Рис. 7.5.2. Частотные функции фильтров.

Произведем проверку работы фильтра на простом массиве данных s_n = n, производная которого постоянна и равна 1. Для массива с постоянной производной фильтр может быть проверен в любой точке массива, в том числе и в точке n=0, для которой имеем:

у = 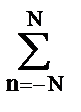h_n s_o-n = 2 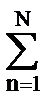n h_n,

при этом получаем: у=0.5512 при N=5, у=1.53 при N=10.

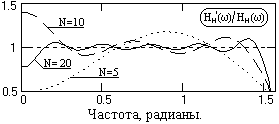Рис. 7.5.3. Погрешность дифференцирования.

Такое существенное расхождение с действительным значением производной объясняется тем, что при w=0 тангенс угла наклона реальных передаточных функций фильтра, как это видно на рисунке 7.5.2, весьма существенно отличается от тангенса угла наклона аппроксимируемой функции H(w) = w. На рис. 7.5.3 приведены частотные графики относительной погрешности дифференцирования s = H_н'(w)/H_н(w) с вычислением значений на нулевой частоте по пределам функций при N → ∞. На рис. 7.5.4 приведен пример операции дифференцирования гармоники s с частотой w_o оператором с N=10 в сопоставлении с точным дифференцированием ds/dk.

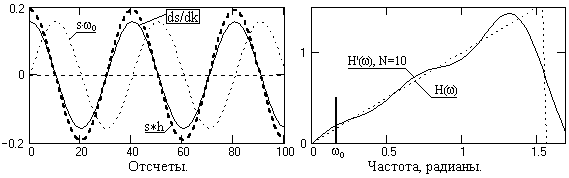
Рис. 7.5.4. Пример операции дифференцирования.

Применение весовых функций. Применим для нейтрализации явления Гиббса весовую функцию Хемминга. Результат нейтрализации для фильтра с N=10 приведен на рис. 7.5.5. Повторим проверочный расчет дифференцирования на массиве s_n = n и получим результат у=1.041, т.е. погрешность дифференцирования уменьшается порядок.

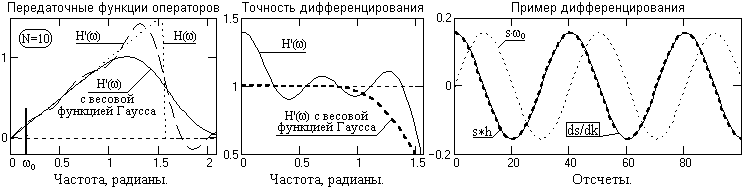
Рис. 7.5.5. Дифференцирование с применением весовой функции.

Аналогично производится расчет и полосовых дифференцирующих фильтров с соответствующим изменением пределов интегрирования в (7.5.1) от w_н до w_в. При этом получаем:

h_n = (w_нcos nw_н-w_вcos nw_в)/(np) + (sin nw_в-sin nw_н)/(n2p).

Фильтры с линейной групповой задержкой. Дифференцирующие фильтры, а равно и любые другие фильтр с мнимой частотной характеристикой, например, оператор преобразования Гильберта, могут быть выполнены в каузальном варианте при условии обеспечения линейной групповой задержки сигнала, которое записывается следующим образом:

j(w) = b - aw, (7.5.4)

где b и a - константы.

Оно выполняется, если импульсная характеристика фильтра имеет положительную симметрию:

h(n) = -h(N-n-1), n = 0, 1, 2, …, (N-1)/2, N – нечетное (тип 1);

n = 0, 1, 2, …, (N/2)-1, N – четное (тип 2).

При этом фазовая характеристика будет определяться длиной фильтра:

a = (N-1)/2, b = p/2.

Частотная характеристика фильтра:

H(w) = |H(w)| exp(jj(w)), (7.5.4)

где модуль |H(w)| задается нечетным. Оба типа фильтров вводят в выходной сигнал сдвиг фазы на 90^о. Кроме того, частотная характеристика фильтра типа 1 всегда равно нулю на частоте Найквиста, что определяется знакопеременностью левой и правой части главного диапазона спектра с учетом периодизации спектра дискретных функций.

Курсовая работа 10-07. Разработать и исследовать оптимальный способ закругления частотной характеристики дифференциального фильтра и реализовать его в программе расчета фильтра и фильтрации цифровых данных..

7.6. АЛЬТЕРНАТИВНЫЕ МЕТОДЫ РАСЧЕТА нцф [43].

Метод прямого расчета НЦФ по частотной характеристики понятен и прост для применения. Недостаток метода – отсутствие гибкости. Он не позволяет проектировать фильтры с разной степенью неравномерности частотной характеристики в полосах пропускания и подавления, а степень неравномерности не зависит от количества членов фильтра и не может изменяться. Максимальные осцилляции частотной характеристики всегда наблюдаются в области полосовых границ и уменьшаются при удалении от них, но при близких границах могут наблюдаться явления интерференции осцилляций. Более гибкими в проектировании являются альтернативные методы: оптимизационные,

Оптимизационные методы позволяют проектировать экономные по размерам операторы фильтров с оптимальными (по Чебышеву) осцилляциями частотных характеристик. Они основаны на понятии полос равных колебаний.

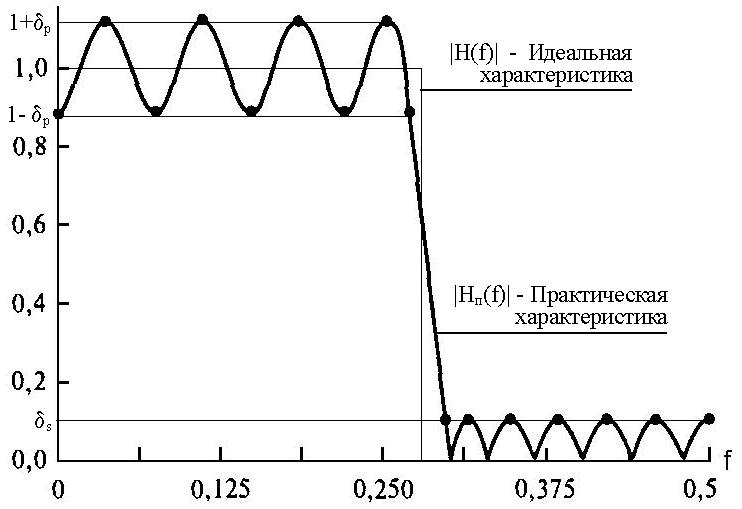Рис. 7.6.1. Оптимальный фильтр низких частот

Частотная характеристика оптимального фильтра низких частот приведена на рис. 7.6.1. В полосе пропускания реальная характеристика фильтра осциллирует с постоянными амплитудными колебаниями между значениями 1-d_p и 1+d_p. В полосе подавления осцилляции постоянной амплитуды находятся в интервале 0-d_s. Разность между идеальной и практической характеристиками представляет собой функцию ошибок E(f). Оптимальный метод позволяет определить коэффициенты фильтра h(n), для которых значение максимальной взвешенной ошибки минимизируется

min[max(E(f))]

в полосе пропускания и в полосе подавления, при этом характеристика фильтра будет иметь равные колебания в пределах полос пропускания и подавления, а количество экстремумов колебаний у фильтров с линейной фазовой характеристикой обычно прямо связано с количеством коэффициентов фильтра (N+1)/2.

При расчете фильтра ключевым моментом является определение положения частот экстремумов, которое выполняется итерационным алгоритмом Ремеза, после чего по положениям экстремумов задается частотная характеристика фильтра и определяются его коэффициенты. Методика расчета оптимальных фильтров подробно с примерами, в том числе в среде Matlab, рассмотрена в работе /43/.

Метод частотной выборки представляет собой вариант метода расчета фильтра по частотной характеристике без применения весовых функций и может применяться для расчетов как частотно-избирательных фильтров, так и фильтров с произвольной частотной характеристикой.

В основе метода лежит непосредственное задание частотной характеристики фильтра в цифровой форме с последующим подбором переходных зон под требуемые характеристики фильтра по величине допустимых осцилляций в полосе пропускания и подавления. Расчет желательно вести в интерактивном режиме, например, в среде Mathcad. В качестве примера приведем расчет низкочастотного фильтра.

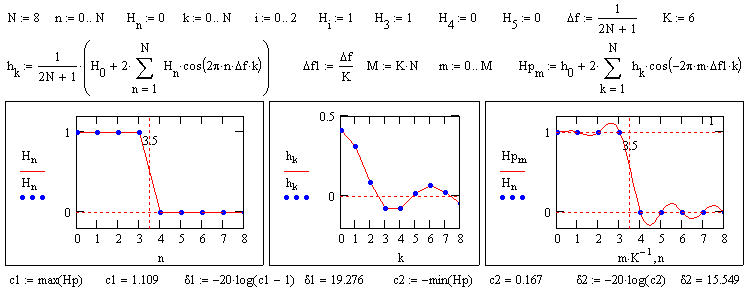Рис. 7.6.2. Задание параметров НЦФ.

Допустим, нам требуется достаточно простой симметричный низкочастотный фильтр с шириной переходной зоны порядка 0.2 главного частотного диапазона (при Dk=1 для фильтра, f_N = 0.5 Гц для спектра и ширина переходной зоны 0.2 х 0.5 = 0.1 Гц). Минимальный размер фильтра при идеальной характеристике для обеспечения такого перехода 2N+1 = 2(1+1/0.1) = 11 точек. С учетом расширения переходной зоны при уменьшении осцилляций на границе зон примем для начала N=8. Частотная характеристика проектируемого фильтра (правая половина) приведена на рис. 7.6.2 с границей раздела зон между 3 и 4 отсчетами спектра. Расчет оператора фильтра проводим обратным преобразованием Фурье, а по полученным отсчетам оператора вычисляем фактическую частотную характеристику этого оператора с уменьшением шага по частоте в 4-6 раз, что позволяет выявить осцилляции и определить погрешность фильтра (по максимумам осцилляций).

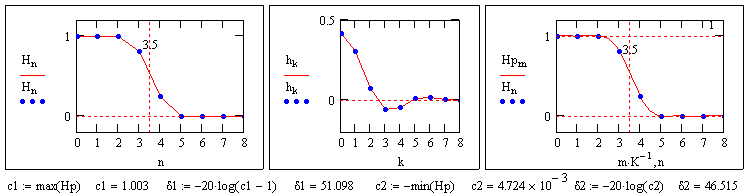Рис. 7.6.3. Подбор отсчетов переходной зоны НЦФ.

На рис. 7.6.3. показан результат подбора частотных значений характеристики фильтра в районе переходной зоны (2 точки), что позволяет более чем в 30 раз снизить осцилляции частотной характеристики.

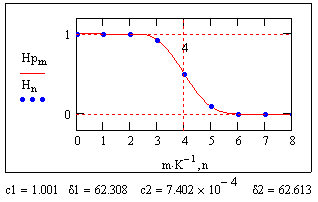Рис. 7.6.4. НЦФ с точкой подбора на границе.

Попутно заметим, что изменение осцилляций характеристики фильтра может производиться индивидуально для зоны пропускания (левой от границы точкой) и зоны подавления (правой точкой) в зависимости от того, требуется ли более высокая точность пропускания или подавления частот. Особенно эффективно это при использовании трех точек подбора с расположением центральной точки на границе полос пропускания и подавления, как это показано на рис. 7.6.4.

При использовании данного метода может использоваться и комбинированный подход: задание на частотной характеристике избыточного количества точек, отладка параметров фильтра по трем и более точкам в переходных зонах, а затем усечение оператора фильтра с применением весовых функций.

Метод частотных выборок допускает также рекурсивную реализацию фильтров /43/.

литература

24. Хемминг Р.В. Цифровые фильтры. – М.: Недра, 1987. – 221 с.

43. Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход. / М., "Вильямс", 2004, 992 с.

Главный сайт автора ~ Лекции по ЦОС ~ Практикум

О замеченных опечатках, ошибках и предложениях по дополнению: davpro@yandex.ru.

Copyright ©2008 Davydov А.V.