Определение. Два неравенства 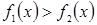 ,
, 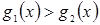 ,
, 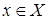 , называют равносильными на некотором множестве
, называют равносильными на некотором множестве 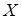 , если их множества решений совпадают.
, если их множества решений совпадают.
Пример. Неравенства 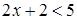 и
и 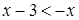 равносильны, так как решением каждого из них служит интервал
равносильны, так как решением каждого из них служит интервал 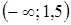 .
.
Определение. Пусть на некотором множестве 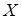 задано неравенство
задано неравенство 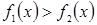 (1). Неравенство
(1). Неравенство 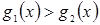 ,
, 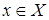 , (2) называют следствием данного неравенства (1), если его множество решений является подмножеством множества решений неравенства (2).
, (2) называют следствием данного неравенства (1), если его множество решений является подмножеством множества решений неравенства (2).
Запись 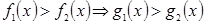 означает, что неравенство (2) есть следствие неравенства (1).
означает, что неравенство (2) есть следствие неравенства (1).
Пример. Неравенство 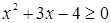 является следствием неравенства
является следствием неравенства 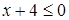 . Так как множество решений второго неравенства
. Так как множество решений второго неравенства 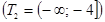 есть подмножество множества решений первого неравенства
есть подмножество множества решений первого неравенства 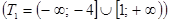 .
.
Два неравенства равносильны тогда, и только тогда, когда каждое из них является следствием другого.
Теорема 2. Если к обеим частям неравенства 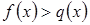 (1), прибавить выражение
(1), прибавить выражение 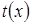 , определенное при всех
, определенное при всех 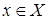 , то получим новое неравенство
, то получим новое неравенство 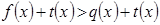 (2), равносильное данному неравенству на множестве
(2), равносильное данному неравенству на множестве 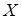 .
.
Доказательство. Покажем, что множества истинности неравенств (1) и (2) совпадают, то есть если 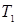 – множество решений неравенства (1),
– множество решений неравенства (1), 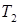 – множество решений неравенства (2), то
– множество решений неравенства (2), то 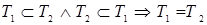 .
.
Пусть 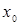 - решение неравенства (1), тогда
- решение неравенства (1), тогда 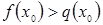 - истинное числовое неравенство. Прибавим к обеим частям этого неравенства
- истинное числовое неравенство. Прибавим к обеим частям этого неравенства 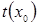 , тогда, по свойству истинных числовых неравенств,
, тогда, по свойству истинных числовых неравенств, 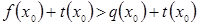 - истинное числовое неравенство.
- истинное числовое неравенство.
Следовательно, 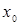 является решением неравенства (2), то есть
является решением неравенства (2), то есть 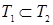 .
.
Пусть теперь 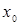 - решение неравенства (2), тогда
- решение неравенства (2), тогда 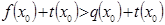 - истинное числовое неравенство. Прибавим к обеим частям выражение, тогда по свойству истинных числовых неравенств:
- истинное числовое неравенство. Прибавим к обеим частям выражение, тогда по свойству истинных числовых неравенств: 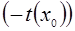 , получим
, получим  - истинное числовое неравенство.
- истинное числовое неравенство.
Следовательно, 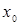 является решением неравенства (1), то есть
является решением неравенства (1), то есть  .
.
Таким образом, 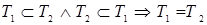 , следовательно, неравенства (1) и (2) равносильны.
, следовательно, неравенства (1) и (2) равносильны.
Ясно, что теорема справедлива и для неравенств вида 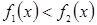 ,
, 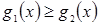 ,
, 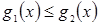 ,
, 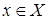 .
.
Следствие. Члены неравенства можно переносить из одной части неравенства в другую с противоположным знаком.
Теорема 3. Если выражение 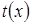 имеет смысл при всех
имеет смысл при всех 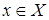 и положительно на
и положительно на 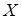 , то неравенства
, то неравенства 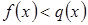 ,
, 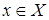 (1) и
(1) и 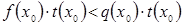 ,
, 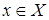 (2), равносильны.
(2), равносильны.
Доказательство. Покажем, что множества истинности неравенств (1) и (2) совпадают, то есть если 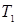 – множество решений неравенства (1),
– множество решений неравенства (1), 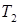 – множество решений неравенства (2), то
– множество решений неравенства (2), то 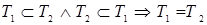 .
.
Пусть 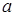 принадлежит
принадлежит 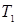 – множеству решений неравенства (1). Тогда справедливо числовое неравенство
– множеству решений неравенства (1). Тогда справедливо числовое неравенство 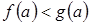 . Но
. Но  – некоторое положительное число, так как по условию
– некоторое положительное число, так как по условию 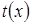 имеет смысл и положительно при всех
имеет смысл и положительно при всех 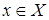 , и, в частности, при
, и, в частности, при 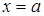 .
.
Умножив обе части верного числового неравенства 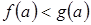 на одно и то же положительное число
на одно и то же положительное число  , получим верное числовое неравенство
, получим верное числовое неравенство 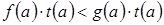 , которое показывает, что
, которое показывает, что 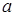 принадлежит и множеству решений неравенства (2). Следовательно,, каждое решение неравенства (1) является решением неравенства (2), то есть
принадлежит и множеству решений неравенства (2). Следовательно,, каждое решение неравенства (1) является решением неравенства (2), то есть 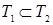 .
.
Пусть теперь 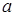 принадлежит
принадлежит 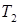 – множеству решений неравенства (2). Тогда
– множеству решений неравенства (2). Тогда 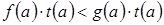 – верное числовое неравенство. Но
– верное числовое неравенство. Но  – некоторое положительное число
– некоторое положительное число 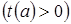 , следовательно, и
, следовательно, и 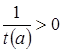 . Умножив обе части верного числового неравенства
. Умножив обе части верного числового неравенства 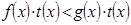 , на одно и то же положительное число
, на одно и то же положительное число 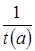 , получим верное числовое неравенство
, получим верное числовое неравенство 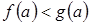 , которое показывает, что
, которое показывает, что 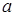 принадлежит
принадлежит 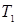 – множеству решений неравенства (1). Следовательно, каждое решение неравенства (2) является решением неравенства (1), то есть
– множеству решений неравенства (1). Следовательно, каждое решение неравенства (2) является решением неравенства (1), то есть 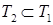 .
.
Таким образом, 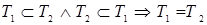 – данные неравенства равносильны.
– данные неравенства равносильны.
Ясно, что теорема справедлива и для неравенств вида 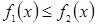 ,
, 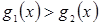 ,
, 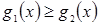 ,
, 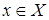 .
.
Следствие. Если обе части неравенства умножить (или разделить) на одно и то же положительное число, получим неравенство, равносильное данному.
Теорема 4. Если 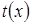 имеет смысл при всех
имеет смысл при всех 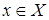 и отрицательно на
и отрицательно на 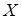 , то неравенства
, то неравенства 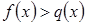 ,
, 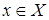 (1) и
(1) и 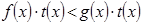 ,
, 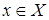 равносильны.
равносильны.
Доказательство данной теоремы опустим.
Следствие. Если обе части неравенства умножить (или разделить) на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.
Приведем некоторые утверждения о равносильности неравенств.
Утверждение 1. Неравенства 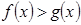 и
и 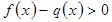 равносильны.
равносильны.
Утверждение 2. Неравенства 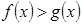 и
и 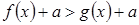 равносильны при
равносильны при 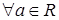 .
.
Утверждение 3. Неравенства 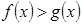 и
и 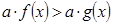 равносильны для
равносильны для 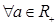 .
.
Утверждение 4. Неравенства 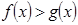 и
и 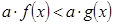 равносильны для
равносильны для 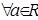 .
.
Утверждение 5. Неравенства 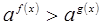 и
и 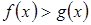 равносильны для любого фиксированного числа
равносильны для любого фиксированного числа 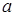 такого, что
такого, что 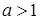 .
.
Утверждение 6. Неравенство  является следствием неравенства
является следствием неравенства 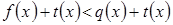 .
.
Утверждение 7. Неравенство  является следствием неравенства
является следствием неравенства 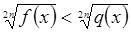 ,
, 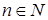 .
.
Ясно, что утверждения справедливы и для неравенств вида 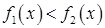 ,
, 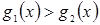 ,
, 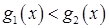 ,
, 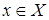 .
.
 2015-07-02
2015-07-02 2953
2953








