Определение. Неравенства вида 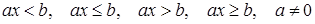 ,
, 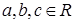 называют линейными неравенствами.
называют линейными неравенствами.
Если 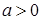 , то неравенство
, то неравенство 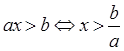 ,следовательно, множество решений данного неравенства есть промежуток
,следовательно, множество решений данного неравенства есть промежуток 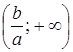 .
.
Если 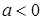 , то неравенство
, то неравенство 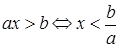 , следовательно, множество решений данного неравенства есть промежуток
, следовательно, множество решений данного неравенства есть промежуток 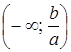 .
.
Если 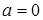 , то неравенство примет вид
, то неравенство примет вид 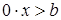 ; оно не имеет решений, если
; оно не имеет решений, если 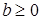 и верно при любых
и верно при любых 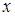 , если
, если 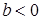 .
.
Решением неравенства может быть подмножество множества, на котором задается неравенство и, как правило, решением неравенства является бесконечное множество, которое иллюстрируется на числовой оси:
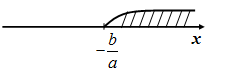
Пример. Решим неравенство: 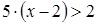 .
.
Решение. 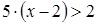 ;
; 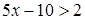 ;
; 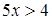 ;
; 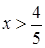 .
.
Дадим иллюстрацию решения неравенства на числовой оси:
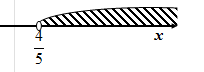
Ответ. 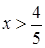 или
или 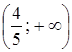 .
.
Пример. Решим неравенство: 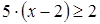 .
.
Решение. 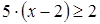 ;
; 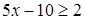 ;
; 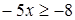 ;
; 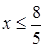 .
.
Дадим иллюстрацию решения неравенства на числовой оси:
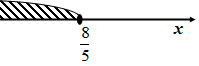
Ответ. 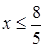 или
или 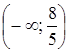 .
.
Пример. Решим неравенство: 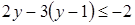 .
.
Решение. 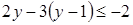 ;
; 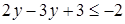 ;
; 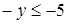 ;
; 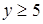 .
.
Ответ. 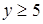 .
.
Пример. Решим неравенство: 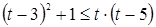 .
.
Решение. 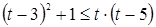 ;
; 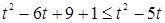 ;
; 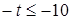 ;
; 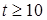 .
.
Ответ. 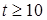 .
.
 2015-07-02
2015-07-02 2265
2265
