2015-07-02
8467
Рассмотрим доказательства некоторых неравенств. Способы доказательства состоят в следующем:
− оказываемое неравенство путём преобразований, основанных на свойствах неравенств и сохраняющих их равносильность, сводят к неравенству, справедливость которого известна;
− путём равносильных преобразований очевидное или известное неравенство сводят к доказываемому неравенству;
− комбинируют первый и второй способы, то есть преобразуют как известное, так и доказываемое неравенства.
Применение данных способов проиллюстрируем примерами.
Пример. Докажем неравенство: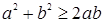 
.
Доказательство. В самом деле, разность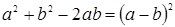 
. Очевидно, что 
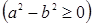, следовательно, 
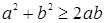, причем равенство достигается только при 
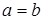. Неравенство доказано.
Пример. Докажем неравенство: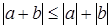 
.
Доказательство. Так как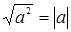 
, 
, 
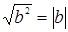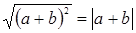, то неравенство принимает вид: 
.
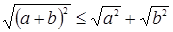Это неравенство приводится возведением в квадрат к равносильному: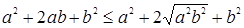 
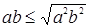, то есть 
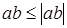, что очевидно.
Заметим, что равенство достигается лишь в случае, когда числа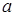 
и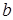 
имеют одинаковые знаки или хотя бы одно из них равно нулю.
Неравенство доказано.
Пример. Докажем неравенство: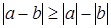 
.
Доказательство. В самом деле,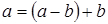 
.
Поэтому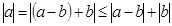 
или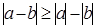 
. Неравенство доказано.
Пример. Докажем неравенство: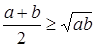 
, если 
.
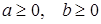Доказательство. Число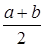 
называют средним арифметическим чисел 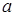и 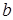, а число 
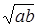– их средним геометрическим.
Другими словами докажем, что среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического.
Для доказательства рассмотрим разность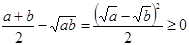 
.
Следовательно,,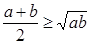 
, причём равенство достигается только при 
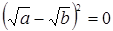, что возможно только при 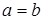. Неравенство доказано.
Замечание. Понятия среднего арифметического и среднего геометрического вводятся и для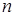 
неотрицательных чисел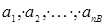 
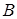этом случае справедливо неравенство: 
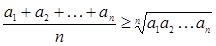, причем равенство достигается лишь при 
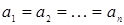. Неравенство доказано.
Пример. Докажем неравенство: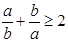 
, есл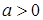и 
и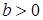 
, причём равенство достигается лишь при .
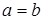Доказательство. В самом деле, числа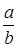 
и 
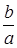положительны. Поэтому среднее арифметическое чисел 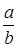и 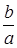не меньше их среднего геометрического: 
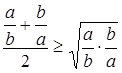или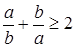 
, равенство только в том случае, когда 
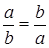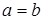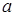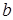, то есть при , так как и – положительны. Неравенство доказано.
Пример. Докажем неравенство: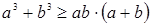 
, если 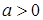, , 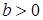причем равенство достигается лишь при .
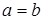Доказательство. В самом деле,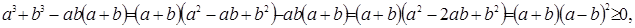 
Неравенство доказано.
Пример. Доказать, что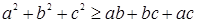 
.
Решение. Складываются три известных неравенства: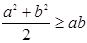 
, 
, 
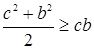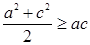. Получаем .
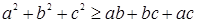Пример. Доказать, что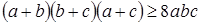 
, если 
.
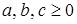Решение. Умножая неравенства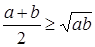 
, 
, 
.
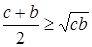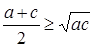Имеем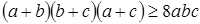 
, так как 
.
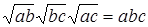Пример. Доказать, что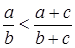 
, есл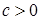и 
и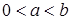 
.
Решение. Используем равносильность неравенств: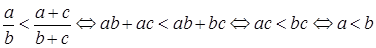 
. Неравенство доказано.
При доказательстве некоторых неравенств удобно использовать замену данных величин другими.
Пример. Доказать, что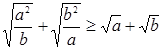 
, если , .
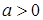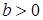Решение. Полагая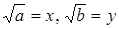 
, запишем неравенство в виде 
, 
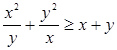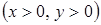, равносильное известному 
.
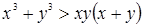Неравенство доказано.
