Понятие неравенства с одной переменной

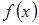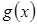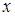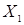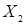Определение. Пусть и – выражения с переменной , определенные соответственно на множестве и . Предикат вида 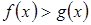, (, 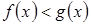, 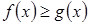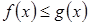), определенный на множестве 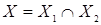, называют неравенством с одной переменной.

При дальнейшем изложении, вместо термина «неравенство с переменной» будем употреблять термин «неравенство».

Определение. Всякое значение переменной 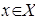, при котором неравенство обращается в верное числовое неравенство, называют решением неравенства.

Иначе говоря, если 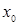– решение неравенства, то число 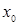– это, то значение переменной 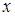, которое обращает неравенство в верное числовое неравенство.

Пример. 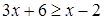– это неравенство с одной переменной. Оно представляет собой два алгебраических выражения соединенных знаком неравенства. Значение 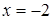является решением данного неравенства, так как данное значение переменной обращает неравенство в верное числовое неравенство: 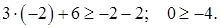‒ верное числовое неравенство.

Решить неравенство – следовательно, найти все его решения или доказать, что их нет.

При дальнейшем изложении будем формулировать определения и утверждения для неравенства 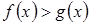. Ясно, что аналогичные определения и утверждения можно сформулировать для неравенств:

, , .

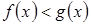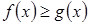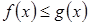Множество всех решений неравенства 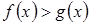(или множество истинности 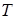предиката 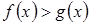), , 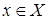принято называть множеством решения неравенства.

Определение. Множество всех чисел, при подстановке которых в неравенство вместо переменной 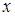, получают верные числовые неравенства, называют множеством решений данного неравенства.

Определение. Множество значений 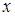, при которых определены обе части неравенства, называют областью определения неравенства (областью допустимых значений переменной ).

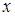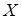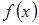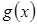Замечание. В дальнейшем, если не оговорено специально, под множеством будем понимать подмножество множества действительных чисел, и будем считать, что, и определены на всем множестве .

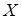Неравенства, содержащие неизвестные величины, также как и уравнения, делят на алгебраические неравенства и трансцендентные. Алгебраические неравенства делят на неравенства первой, второй и т.д. степени.

Пример. Неравенство 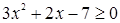– алгебраическое неравенство, второй степени. Неравенство 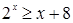– трансцендентное неравенство.