Решение неравенств и систем неравенств с двумя переменными

Определение. Пусть 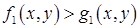– неравенство, определенное на множестве 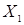; 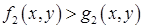– неравенство, определенное на множестве 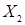и т.д. 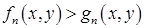– неравенство, определенное на множестве .

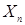Конъюнкцию предикатов 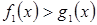; ; 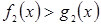…; 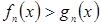называют системой данных неравенств и записывают: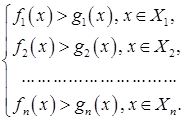

Аналогично определяют систему неравенств со знаками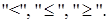

Областью определения системы неравенств с одной переменной называют множество .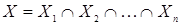

Значения переменной, при которой каждое неравенство системы обращается в верное числовое неравенство, называют решением системы неравенств.

Решить систему неравенств следовательно, найти все решения этой системы или установить, что их нет.

Множеством решений системы неравенств является пересечение множеств решений неравенств, образующих систему.

Две системы неравенств называются равносильными, если всякое решение одной из них является решением другой, и наоборот.

Если обе системы неравенств не имеют решений, то их тоже считают равносильными.

Решением неравенства с двумя переменными называют пару значений переменных, обращающую каждое неравенство в верное числовое неравенство.

Решением систем неравенств с двумя переменными является упорядоченная пара чисел, удовлетворяющая каждому неравенству системы.

Множество решений системы неравенств – это пересечение множеств решений всех неравенств, входящих в систему.

Поскольку пара действительных чисел 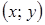однозначно определяет точку координатной плоскости, то это дает возможность изобразить решение неравенства или системы неравенств с двумя переменными графически.

Теорема 5. В каждой из областей 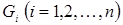, на которые линия 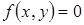делит координатную плоскость, функция 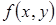либо положительна, либо отрицательна.

Каждое неравенство системы определяет некоторую область 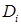плоскости 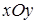, в которой лежит контрольная точка, в противном случае решением неравенства является область, не содержащая контрольную точку. В качестве контрольной точки удобно выбирать начало координат .

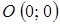Пример. Найдем полуплоскость, определяемую неравенством .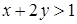

Решение. Построим прямую 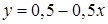.Данная прямая не проходит через начало координат. Следовательно, в качестве контрольной точки для решения неравенства 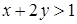целесообразно взять точку .

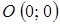Подставим координаты точки 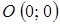в неравенство, получим неверное числовое неравенство 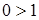. Следовательно, точка 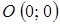не принадлежит области решений неравенства. Другими словами, полуплоскость, определяемая неравенством, не содержит точку 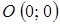. На рисунке 14 искомая полуплоскость заштрихована.

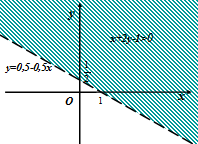Рис.14

В общем случае множество решений системы неравенств представляет собой ограниченную или неограниченную область плоскости 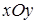, линию, точку, пустое множество.

Пример. Решим графически систему неравенств: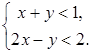

Решение. Так как 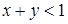, то 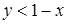; так как 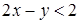, то 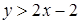. Строим прямые 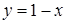и 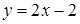(Рис.15).

Множество решений неравенства 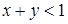состоит из точек плоскости, лежащих под прямой 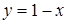, а неравенство 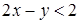– из точек, лежащих над прямой 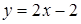(Рис.15), то есть множество решений каждого из этих линейных неравенств есть полуплоскость.

Графически решение данной системы неравенств есть пересечение полуплоскостей, не включая границу (Рис.15).

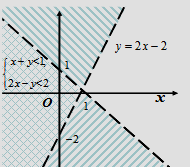Рис.15

Пример. Изобразим на координатной плоскости множество решений неравенства .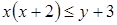

Решение. Преобразуем неравенство к виду: 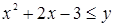. Построим на координатной плоскости параболу 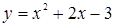. Парабола разбивает плоскость на две област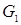и и 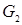. 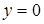: 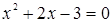; ; 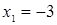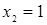(Рис. 16).

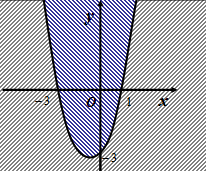
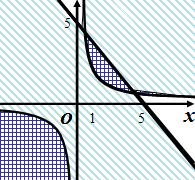
Рис.16 Рис.17

Решением неравенства является множество точек плоскости, лежащих выше параболы 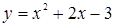и поскольку неравенство 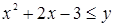нестрогое, то в решение неравенства входит множество точек плоскости, лежащих на параболе .

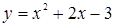Решение данной системы неравенств представлено на рисунке 16.

Пример. Изобразим на координатной плоскости множество решений системы неравенств: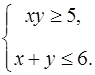

Решение. , .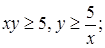

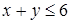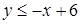Геометрически, решением системы неравенств 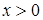, 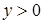является множество точек первого координатного угла (Рис.17).

Решением неравенства 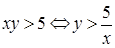поскольку 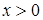, является множество точек лежащих выше ветви гиперболы, служащей графиком функции .

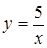Решением неравенства 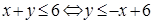является множество точек, лежащих ниже прямой и на прямой, служащей графиком функции .

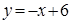Решение данной системы неравенств представлено на рисунке 17.

Пример. Решим графически систему неравенств: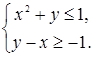

Решение. Построим параболу 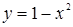и прямую 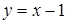. Множество, заданное системой неравенств, состоит из точек, лежащих на параболе 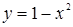или под ней и одновременно на прямой 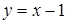или над ней.

Решение данной системы неравенств представлено на рисунке 18.

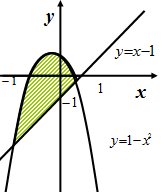
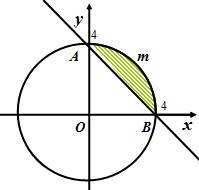
Рис.18 Рис.19

Пример. Решим графически систему двух неравенств: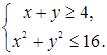

Решение. Решением первого неравенства являются точки полуплоскости с границей 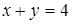, включая эту прямую. Решением второго неравенства является внутренность круга с центром в начале координат и радиусом, равным 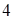, включая точки окружности, которая является границей круга.

Решением системы неравенств является множество точек координатной плоскости, ограниченное дугой 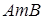окружности 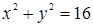и прямой 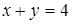. Решение данной системы неравенств представлено на рисунке 19.