Для графического решения неравенства 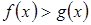 нужно построить график функций
нужно построить график функций 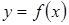 и
и 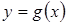 , выбрав те промежутки оси абсцисс, на которых график функции
, выбрав те промежутки оси абсцисс, на которых график функции 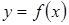 расположен выше графика функции
расположен выше графика функции 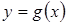 .
.
Пример. Решим графически неравенство 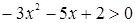 .
.
Решение. График функции 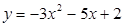 – парабола, ветви которой направлены вниз. Корни трехчлена:
– парабола, ветви которой направлены вниз. Корни трехчлена: 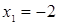 и
и 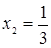 , поэтому парабола пересекает ось
, поэтому парабола пересекает ось 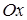 в данных точках.
в данных точках.
График функции 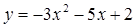 схематически изображен на рисунке 11. Неравенству
схематически изображен на рисунке 11. Неравенству 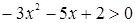 удовлетворяют те значения
удовлетворяют те значения 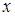 , при которых точки параболы лежат выше оси
, при которых точки параболы лежат выше оси 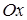 , то есть такие числа
, то есть такие числа 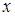 , что
, что 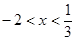 .
.
Можно решить графически и систему неравенств с одним неизвестным.
Пример. Решим графически систему неравенств: 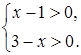
Решение. Построим в одной системе координат графики функций 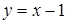 и
и 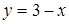 (Рис.12).
(Рис.12).
Оба графика лежат выше оси 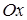 при значениях
при значениях 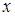 из интервала
из интервала 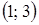 – решения системы неравенств.
– решения системы неравенств.
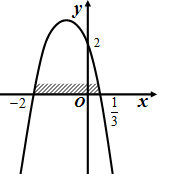
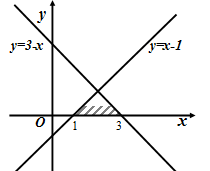
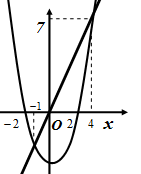
Рис. 11 Рис.12 Рис.13
Пример. Решим графически неравенство 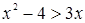 .
.
Решение. Построим в одной системе координат графики функций 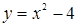 и
и 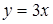 (Рис.13).
(Рис.13).
Из рисунка 13 видно, что график функции 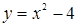 расположен выше графика функции
расположен выше графика функции 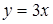 при
при 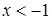 и
и 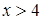 , то есть множество решений исходного неравенства есть множество
, то есть множество решений исходного неравенства есть множество 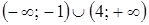 .
.
 2015-07-02
2015-07-02 8553
8553
