Неравенство второй степени с одним неизвестным

(квадратное неравенство)

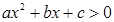
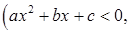
Определение. Неравенство вида 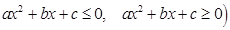, где 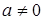, называют квадратным неравенством.

Чтобы решить квадратное неравенство вида 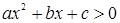, , 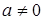достаточно узнать, при каких значениях 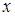график трехчлена находится в верхней полуплоскости, для чего необходимо вычислить дискриминант квадратного трёхчлена: .

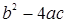Если 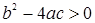, то данному неравенству удовлетворяют все числа, больше большего корня и меньше меньшего корня.

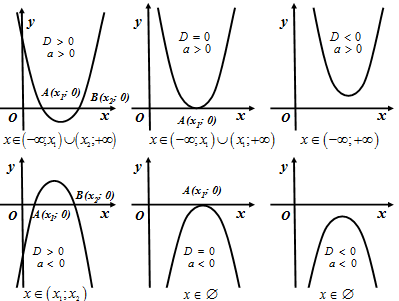Рис.8

Если 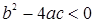, то неравенству удовлетворяют все .

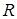Если 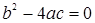, то неравенству будут, удовлетворят все 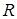, кроме .

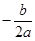Неравенству 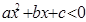, , 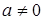при 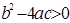удовлетворяют все те значения 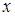, которые больше меньшего корня трехчлена, но меньше большего корня.

Если 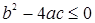, то неравенство не имеет решений.

Пусть 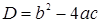, 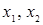– корни квадратного трехчлена.

Графическая иллюстрация решения неравенства 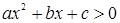представлена на рисунке 8.

Пример. Решим неравенство .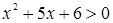

Решение. Найдем дискриминант квадратного трехчлена 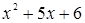, , 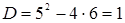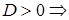квадратный трехчлен имеет два корня. Найдем корни, решив уравнение 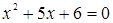, 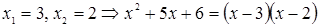. Исходное неравенство равносильно неравенству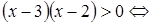

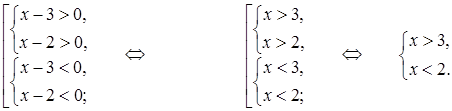
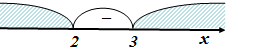
Следовательно, множество решений неравенства 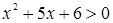есть множество .

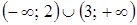Пример. Решим неравенство .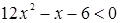

Решение. Рассмотрим функцию 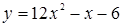. Графиком функции является парабола, ветви которой направлены вверх. Найдем нули функции, решив уравнение 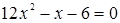, имеем .

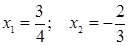График функции 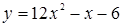схематически изображен на рисунке 9. Очевидно, что 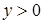при .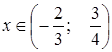

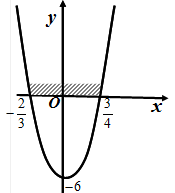Рис.9 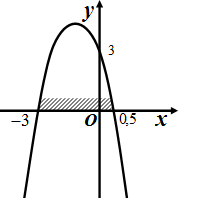Рис.10

Пример. Решим графически неравенство: .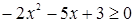

Решение. Рассмотрим функцию 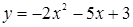. Графиком является парабола, ветви которой направлены вниз. Решив уравнение 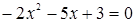, находим нули функци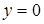и: при 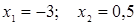. График функции 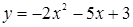схематически изображен на рисунке 10.

Очевидно, что 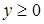при 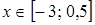. Следовательно, множество решений неравенства 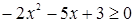есть отрезок .

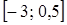Пример. Решим неравенство .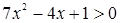

Решение. 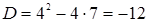, 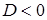. Коэффициент 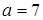больше нуля, таким образом, решением неравенства 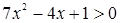является любое .

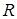Ответ. .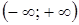

Пример. Решим неравенство .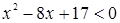

Решение. Найдем дискриминант квадратного трехчлена 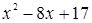. 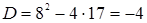, , 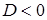коэффициент 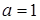больше нуля, следовательно, неравенство 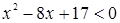, не имеет решений.