Теорема Коші

Теорема. Якщо функції f(x) i j(x) неперервні на [a, b] і мають похідні в інтервалі (a, b) і j¢(х)¹0 для х є (a, b), то існує точка 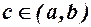, така, що має місце співвідношення:

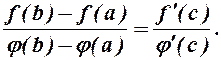(1)

Доведення. Розглянемо допоміжну функцію

,

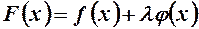де число 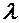підберемо таким, щоб функція 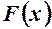задовольняла теорему Ролля.

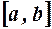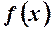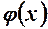Із неперервності на функцій і випливає, що 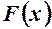теж неперервна. Крім того, із диференційовност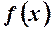і і 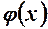в інтервалі 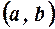випливає диференційовність 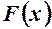. Залишилось знайти число 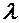таким, щоб 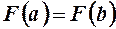, тобто

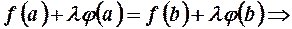
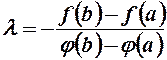. (2)

Отже, згідно з теоремою Ролля існує точка 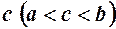, така що 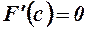, тобто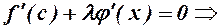

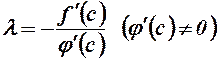. (3)

Із рівностей (2) і (3) отримуємо формулу Коші (1).