Правило Лопіталя

Теорема 1. Нехай функції f(x) i j(x) визначенні і мають похідну в околі точки х₀, а в точці х₀ 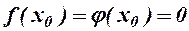, тоді якщо існує границя 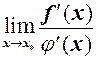, то існує границя ,

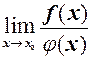причому виконується рівність

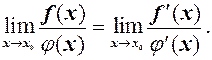
Доведення. Функці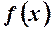ї і 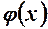задовольняють умовам теореми Коші в околі точки 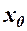, тому

,

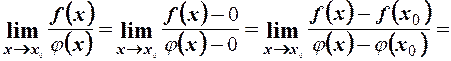
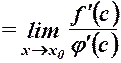де при 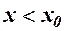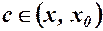, а при .

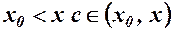Отже, якщо 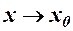, то і 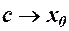, тому

.

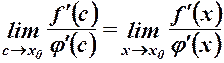В останньому виразі замість змінної 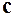можна записати змінну 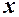, оскільки границя не залежить від позначення змінної.

За допомогою теореми 1 можна розкривати невизначеність вигляду 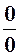, причому правило Лопіталя можно застосовувати повторно, якщо в процесі функції і їх похідні задовольняють умовам теореми.

У випадку невизначеності 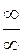користуються такою теоремою.

Теорема 2. Нехай f i j визначені і мають похідну в околі точки

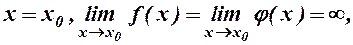причому j(х), j¢(х)¹0 в цьому околі, тоді, якщо існує 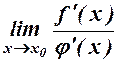, то існує 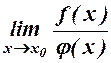і

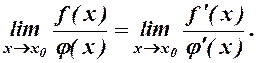
До викладеного додамо, що правило Лопіталя залишається справедливим при .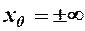

Зауваження. За допомогою теорем 1 і 2 розкриваються такі невизначеності:

1. 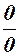і .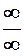

2. Невизначеност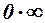і і 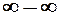за допомогою алгебраїчних перетворень зводяться до вигляду 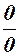або .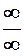
3. Невизначеност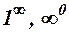і і 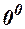за допомогою логарифмування зводяться до невизначеності .

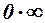Далі ці випадки розглянемо на прикладах.