Застосовуючи правило Лопіталя знайти границі:
1. 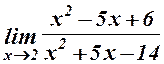 . 2.
. 2. 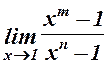 .
.
3. 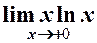 . 4.
. 4. 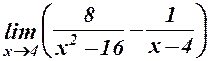 .
.
5. 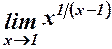 . 6.
. 6. 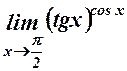 .
.
Розв’язання
1. 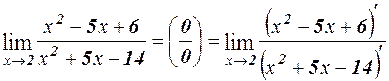
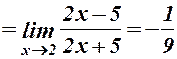 .
.
2. 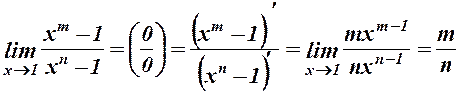 .
.
3. 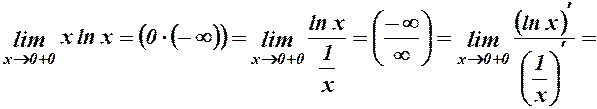
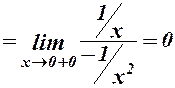 .
.
4. 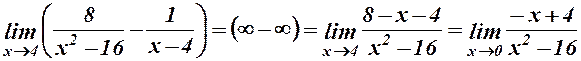
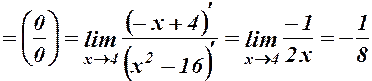 .
.
5. 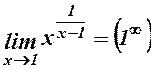 .
.
Позначимо 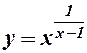 , а потім про логарифмуємо
, а потім про логарифмуємо 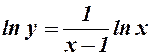 і знайдемо границю
і знайдемо границю
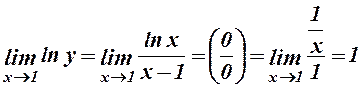 .
.
Оскільки для неперервної функції
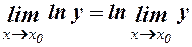 ,
,
то в даному випадку 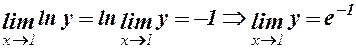 . Отже,
. Отже, 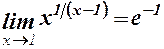 .
.
6. 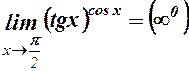 . Покладемо
. Покладемо 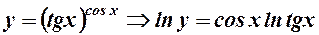 , тоді
, тоді 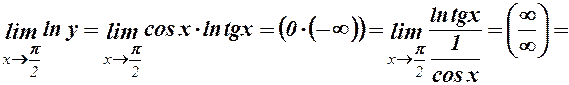
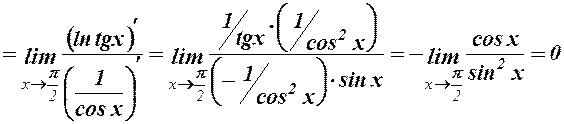 ,
,
тобто
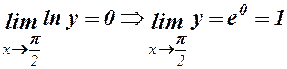 .
.
Приклади для самостійного розв’язання
1. 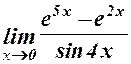 . 2.
. 2. 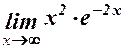 . 3.
. 3. 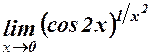
4. 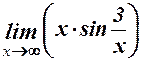 . 5.
. 5. 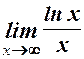 . 6.
. 6. 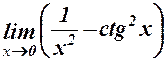 .
.
7. 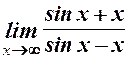 . 8.
. 8. 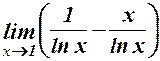 .
.
Відповіді:
1. 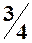 . 2.
. 2. 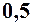 . 3.
. 3. 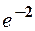 . 4.
. 4. 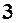 . 5.
. 5. 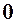 . 6.
. 6. 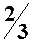 . 7.
. 7. 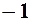 . Вказівка. Невизначеність
. Вказівка. Невизначеність 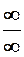 розкрити шляхом по членного ділення чисельника і знаменника на
розкрити шляхом по членного ділення чисельника і знаменника на 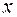 . Правило Лопітааля не підходить оскільки не існує
. Правило Лопітааля не підходить оскільки не існує 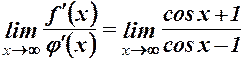 . 8.
. 8. 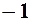 .
.
VII. Дослідження функцій
 2015-07-03
2015-07-03 353
353








