VI. Теореми про диференційовні функції
Теорема. Якщо функція 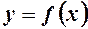 неперервна на відрізку
неперервна на відрізку 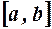 , диференційовна в інтервалі
, диференційовна в інтервалі 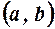 і приймає рівні значення на його кінцях, тобто
і приймає рівні значення на його кінцях, тобто 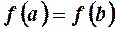 , то в інтервалі
, то в інтервалі 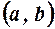 існує хоча б одна точка
існує хоча б одна точка 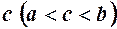 така, що
така, що 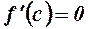 .
.
Геометрично: знайдеться точка С така, що дотична з цією абсцисою до графіка паралельна осі ОХ (див. рис.39)


 Y
Y

 |
f(a) f(b)
 a с1 с2 b X
a с1 с2 b X
Рис.39
Доведення. Оскільки функція 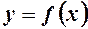 неперервна на
неперервна на 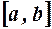 , то вона досягає на цьому відрізку свого найменшого і найбільшого значень. Якщо б ці значення досягались на кінцях відрізка в точках
, то вона досягає на цьому відрізку свого найменшого і найбільшого значень. Якщо б ці значення досягались на кінцях відрізка в точках 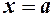 і
і 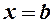 , то за умовою теореми
, то за умовою теореми 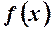 неперервна і
неперервна і 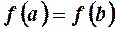 випливало б, що функція
випливало б, що функція 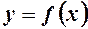 - стала і тоді
- стала і тоді 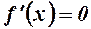 в кожній точці відрізка
в кожній точці відрізка 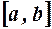 . Тому припускаємо, що функція
. Тому припускаємо, що функція 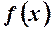 досягає свого, наприклад, найбільшого значення у деякій точці
досягає свого, наприклад, найбільшого значення у деякій точці 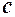
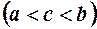 (див. рис. 39),
(див. рис. 39), 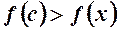 .
.
Обчислимо ліву похідну 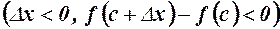
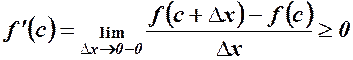 (1)
(1)
і праву похідну 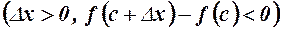
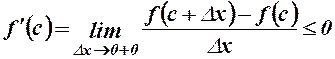 (2)
(2)
Згідно диференційовності 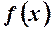 її ліва і права похідні збігаються, тому із співвідношень (1) і (2) випливає, що
її ліва і права похідні збігаються, тому із співвідношень (1) і (2) випливає, що 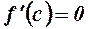 .
.
З рис. 39 видно, що можливі і інші точки, в яких похідна дорівнює нулю 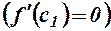 .
.
 2015-07-03
2015-07-03 278
278







