Теорема 1. зростає

1) Якщо функція f(x), яка має похідну в інтервалі (a, b), зростає на [a, b], то її похідна в інтервалі (a, b) невід’ємна, тобто ¦¢(х)³0.

2) Якщо функція f(x) неперервна на відрізку [a, b] і має похідну в (a, b), причому ¦¢(х)>0 для a<x<b, то ця функція зростає на [a, b].

Y

a

рис.40 X

Скорочено можна записати:

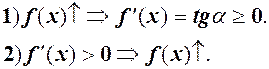
Доведення. 1. Нехай 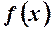зростає і в околі точки 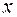існує скінчена похідна 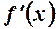. Розглянемо ліву похідну в цій точці

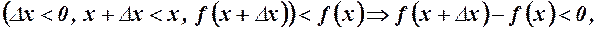
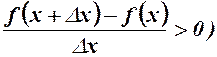
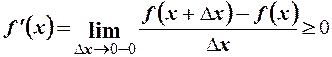
та праву похідну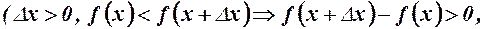

.

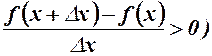
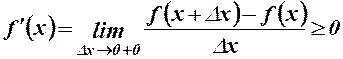Оскільки ліва і права похідні збігаються в точці 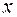, то із останніх нерівностей випливає .

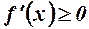2. Нехай в околі точки 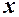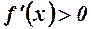. Застосуємо до різниці 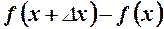формулу Лагранжа

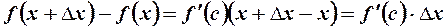. (1)

Розглянемо два випадки. а) 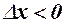, тоді 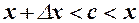і права частина 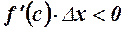, тобто із (1) випливає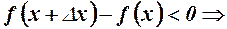

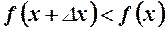- функція зростає

б) 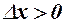, тод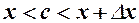і і 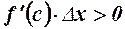, із (1) маємо 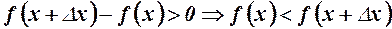- функція зростає.

Отже, в околі точки 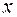(як зліва так і справа) функція зростає, якщо .

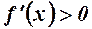Аналогічна теорема має місце, якщо функція f(x) спадає.