1. Функція 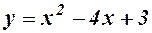 визначена для
визначена для 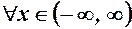 . Знаходимо похідну
. Знаходимо похідну 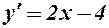 . Похідна точок розриву немає і може змінювати знак при переході через корінь
. Похідна точок розриву немає і може змінювати знак при переході через корінь
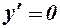 ,
, 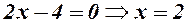 .
.
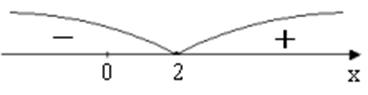 Наносимо корінь
Наносимо корінь 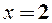 на числову вісь, яка при цьому розіб’ється на два інтервали
на числову вісь, яка при цьому розіб’ється на два інтервали 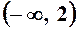 і
і 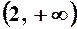
(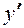 )
)
За допомогою пробних точок визначаємо знак похідної на кожному з інтервалів. Якщо взяти 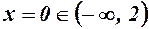 , то
, то 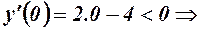
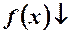 - функція спадає.
- функція спадає.
Якщо 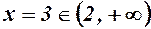 , то
, то
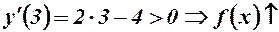 - функція зростає.
- функція зростає.
Отже, для 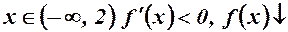 ;
;
для 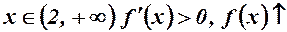 .
.
2. 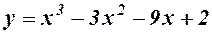 -функція визначена для всіх
-функція визначена для всіх 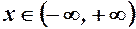 . Її похідна
. Її похідна
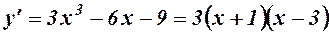
має корені 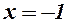 і
і 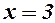 , які розбивають числову вісь на три інтервали
, які розбивають числову вісь на три інтервали
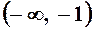 ,
, 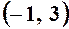 ,
, 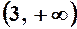
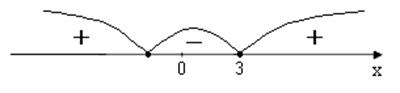
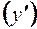
Підставляючи пробні точки у розклад похідної на множники 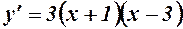 , визначаємо її знак у кожному із інтервалів (див. рис.). У відповідності до знаку похідної на даному інтервалі робимо висновок про поведінку функції:
, визначаємо її знак у кожному із інтервалів (див. рис.). У відповідності до знаку похідної на даному інтервалі робимо висновок про поведінку функції:
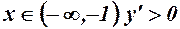 , функція зростає;
, функція зростає;
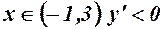 , функція спадає;
, функція спадає;
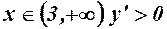 , функція зростає.
, функція зростає.
3. 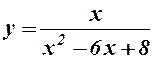 - функція не існує у точках
- функція не існує у точках 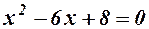
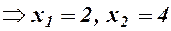 . Знаходимо похідну
. Знаходимо похідну
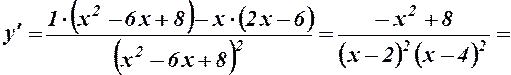
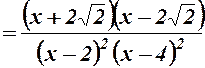 .
.
Корені похідної 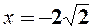 ,
, 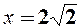 та її точки розриву
та її точки розриву 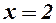 і
і 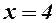 розбивають числову вісь на 5 інтервалів, визначаємо знак похідної на кожному з них:
розбивають числову вісь на 5 інтервалів, визначаємо знак похідної на кожному з них:
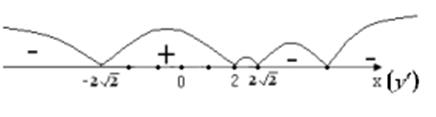
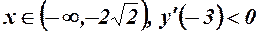 , функція спадає;
, функція спадає;
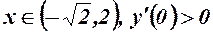 , функція зростає;
, функція зростає;
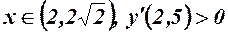 , функція зростає;
, функція зростає;
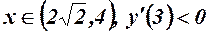 , функція спадає;
, функція спадає;
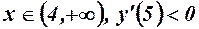 , функція спадає.
, функція спадає.
Тут числа 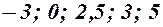 - це пробні точки, з відповідних інтегралів, у яких визначався знак похідної.
- це пробні точки, з відповідних інтегралів, у яких визначався знак похідної.
4. Функція 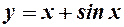 існує для всіх
існує для всіх 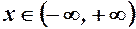 , її похідна
, її похідна
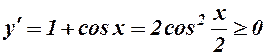 .
.
Оскільки похідна невід’ємна, то дана функція неспадна для всіх 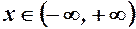 .
.
5. Знайдемо спочатку область існування (визначення) функції 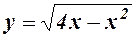 ,
,
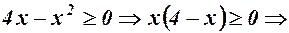
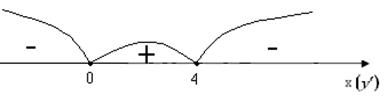
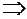 . Функція існує на проміжку
. Функція існує на проміжку 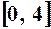 . Похідна функції має вигляд
. Похідна функції має вигляд
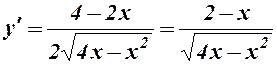 ;
;
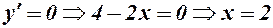 - корінь похідної, яка до того має таку область існування
- корінь похідної, яка до того має таку область існування 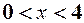 .
.
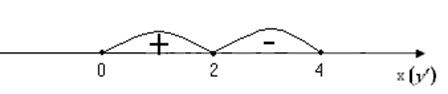
Для 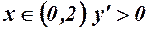 , функція зростає;
, функція зростає;
Для 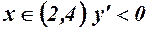 , функція спадає.
, функція спадає.
Відмітимо ще, що за допомогою похідної можна доводити деякі нерівності.
Приклади. Довести нерівності.
6. 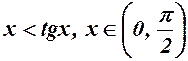 . 7.
. 7. 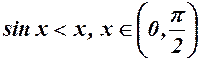 .
.
8. 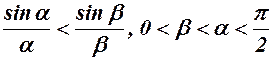 .
.
9. 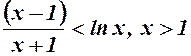 .
.
 2015-07-03
2015-07-03 324
324








