6. Розглянемо допоміжну функцію 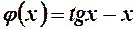 . Знайдемо її похідну
. Знайдемо її похідну
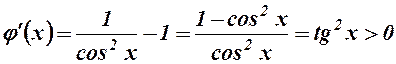 , якщо
, якщо 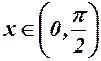 .
.
Отже, 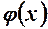 - зростає і
- зростає і 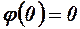 , тобто для
, тобто для 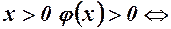
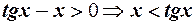 . Геометрично, якщо побудувати графіки
. Геометрично, якщо побудувати графіки 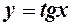 і
і 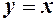
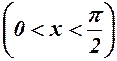 , то тангенсоїда знаходиться вище бісектриси, в точці
, то тангенсоїда знаходиться вище бісектриси, в точці 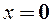 вони дотикаються.
вони дотикаються.
7. Знайдемо похідну для допоміжної функції 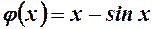 ,
, 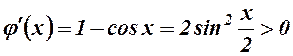 для
для 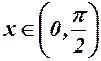 . Функція
. Функція 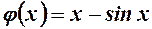 зростає для
зростає для 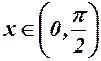 . У точці
. У точці 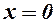
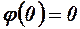 , а внаслідок зростання
, а внаслідок зростання 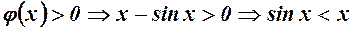 , якщо
, якщо 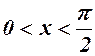 .
.
8. Розглянемо допоміжну функцію 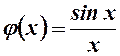 ,
, 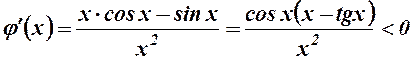 , якщо
, якщо 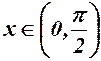 , оскільки
, оскільки 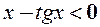 (див. приклад 6). Функція
(див. приклад 6). Функція 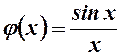 - спадна, тобто меншому значенню аргумента
- спадна, тобто меншому значенню аргумента 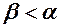 відповідає більше значення функції
відповідає більше значення функції
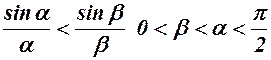 .
.
9. 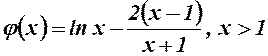 .
.
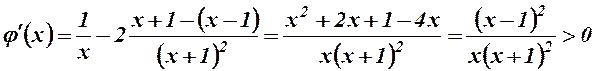 ,
,
якщо 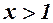 . Функція
. Функція 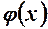 зростає, в точці
зростає, в точці 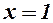
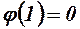 . Отже, для
. Отже, для 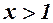
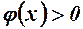 , тобто
, тобто
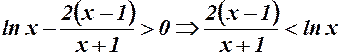 при
при 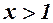 .
.
Приклади для самостійного розв’язання.
Визначити проміжки монотонності функцій
1. 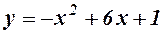 . 2.
. 2. 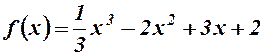 .
.
3. 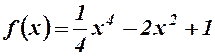 . 4.
. 4. 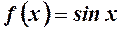 .
.
5. 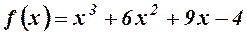 . 6.
. 6. 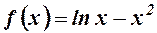 .
.
7. 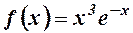 . 8.
. 8. 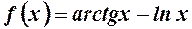 .
.
9. 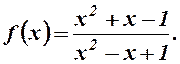
Довести нерівності
10. 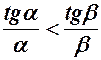 , якщо
, якщо 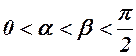 .
.
11. 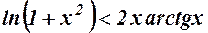 .
.
12. 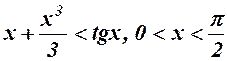 .
.
13. 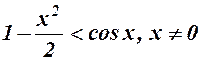 .
.
Відповіді. 1. 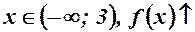 ;
; 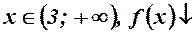 .
.
2. 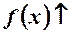 , якщо
, якщо 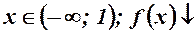 , якщо
, якщо 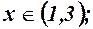
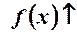 ,
, 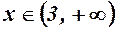 . 3.
. 3. 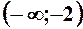 ,
, 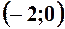 ,
, 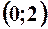 ,
, 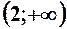 . 4.
. 4. 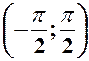 ,
, 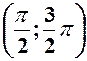 ,
, 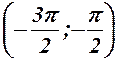 і т. д. 5.
і т. д. 5. 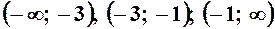 .
.
6. 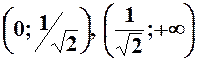 . 7.
. 7. 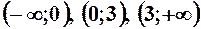 . 8.
. 8. 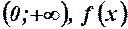 .
.
9. 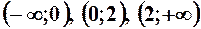 .
.
 2015-07-03
2015-07-03 472
472








