Термодинамика устойчивость нелинейных кинетических систем

Проследим взаимосвязь изменения характера устойчивости сильнонелинейной кинетической системы с изменением ее тер­модинамических свойств при соответствующем изменении неко­торых внешних "управляющих" параметров системы. В качестве изменяющегося параметра для химически активной системы це­лесообразно выбрать значение, например, текущего химического сродства некоторого брутто-процесса или пропорциональные это­му сродству величины, которые характеризовали бы удаленность системы от положения равновесия.

Выше было показано, что вблизи термодинамического равно­весия в системе невозможны периодические процессы. Следова­тельно, на фазовых диаграммах устойчивое стационарное состоя­ние н системах, находящихся в области линейной термодинамики, характеризуется особой точкой, для которой эволюция системы при незначительном отклонении из этой точки обязательно приведет систему снова в эту же точку (рис. 17.2 демонстрирует возвраще­ние системы в точку с прежней скоростью диссипации энергии).

Существенно при этом, что в сильно нелинейных системах при фиксирова иных внешних параметрах возможно существование да­же не одного, а сразу нескольких стационарных состояний

Если эволюция нелинейной системы описывается только од­ним внутренним параметром (например, одним интермедиатом), возможны только устойчивость или неустойчивость системы, но периодические процессы (осцилляции) в ней невозможны. При этом эволюция во время возникшей в системе флуктуации X этого внутреннего параметра дописывается некоторым выражением

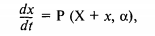
которое вблизи стационарного значения X приводит к линей­ному выражению

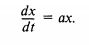
Здесь а — некоторый эффективный коэффициент, зависящий от значения управляющего параметра а. Очевидно, что величина флуктуации растет во времени и, следовательно, система стано­вится неустойчивой при а > 0.

Простейшая система с двумя стационарными состояниями, бифуркацией и неустойчивостью стационарного состояния

Рассмотрим кинетически необратимый брутто-процесс

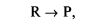
осуществляющийся по нелинейной схеме

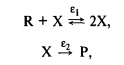
где К и Р — исходный реагент и конечный продукт, а X — интермедиа!-автоката-лнзатор.

Введение кинетической необратимости во второй стадии сразу означает, что эта стадия далека от термодинамического равнове­сия и поэтому для рассматриваемой системы можно ожидать не­устойчивости стационарных состояний. Проверим это.

В стационарном состоянии

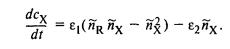
Следовательно, стационарному состоянию отвечают два решения:

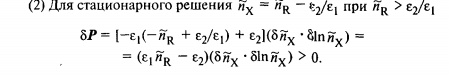
48. Пространственные диссипативные структуры

Пространственные диссипативные структуры.

Диссипативная система (или диссипативная структура) — это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне. Диссипативная система иногда называется ещё стационарной открытой системой или неравновесной открытой системой. Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем — несохранение объёма в фазовом пространстве. Различают пространственные, временные и пространственно-временные диссипативные структуры,.
Простейшим примером пространственных диссипативных структур являются ячейки Бернара. Если горизонтальный слой жидкости сильно подогреть снизу, то между нижней и верхней поверхностями возникает разности температур ∆Т = Т₁-Т₂>0 (рис.18.5,а). При малой разности температур ∆Т, ниже некоторого критического значения ∆Т_кр, подводимое снизу тепло распространяется вверх путем теплопроводности и жидкость остается неподвижной. При разности температур выше критической ∆Т>∆Т_кр в жидкости начинается конвекция: холодная жидкость опускается вниз, а нагретая поднимается вверх. Распределение этих двух противоположно направленных потоков оказывается самоорганизованным (рис. 18.5,а), в результате чего возникает система правильных шестиугольных ячеек (рис.18.5,б)

По краям каждой такой ячейки жидкость опускается вниз, а в центре поднимается вверх. Качественная зависимость полного теплового потока J_Q в единицу времени от нижней поверхности к верхней от разности температур ∆Т изображена на рис. 18.6. При ∆Т > ∆Т_кр состояние неподвижной теплопроводящей жидкости становится неустойчивым (пунктирная линия на рис 18.6), и вместо него наступает новый устойчивый режим в виде конвекционных ячеек Бенара. Обусловлено это тем, что при большоей разности температур покоящаяся жидкость уже не обеспечивает перенос возросшего количества теплоты, поэтому вынужденно устанавливается новый конвекационный режим, обеспечивающий необходимый перенос теплоты в результате упорядоченного движения жидкости.
Очевидно, что этот перенос теплоты является здесь сопрягающим процессом по отношению к установлению сопряженного конвективного процесса. При этом роль управляющего параметра α здесь играет разность температур ∆Т, точка ∆Т_кр соответсвует точке бифуркации.
При переходе от докритического к надкритическому режиму спонтанно меняется симметрия системы, что аналогично термодинамическим фазовым переходам. Именно поэтому переходы с образованием пространственных диссипативных структур в неравновесных системах называют кинетическими фазовыми переходами.
Диссипативные структуры возникают лишь в сильнонеравновесных многочастичных система, состояние которых описывается нелинейными уравнениями для макроскопических величин. Для описания возникновения ячеек Бенара в жидкости используют нелинейные дифференциальные уравнения гидродинамики с анализом неустойчивости решений этих уравнений по Ляпунову. Исследования показывают, что при ∆Т>∆T_кр состояние системы, исходно соответствующее покоящейся жидкости с обычным режимом теплопередачи, становится неустойчивым, и жидкость переходит в новый устойчивый конвекционный режим.
Другим классическим примером пространственных диссипативных структур является так называемая решетка вакансионных пор. Известно, что облучение металла некоторыми частицами (нейтронами, быстрыми ионами) приводит к образованию в кристаллической решетке точечных дефектов – вакансий и межузельных атомов. При повышении температуры эти вакансии, перемещаясь в кристалле, образуют сложные кластеры дефектов в виде сферических вакансионных пор и плоских дислокационных петель. Обычно такие кластеры создают пространственно однородную систему. Однако при определенных условиях облучения вакансионные поры располагаются упорядоченно в виде правильных «сверхрешеток», тип которых совпадает с типом кристаллической решетки металла, с периодом, в сотни раз превышающим период этой решетки. Образование таких упорядоченных структур из вакансионных пор вызвано нелинейным динамическим взаимодействием точечных дефектов с мелкими вакансионными кластерами и диффузионным взаимодействием между порами.
Сходное пространственное структурирование наблюдают в запыленной плазме, когда сильно ионизированные твердые наночастицы образуют устойчивую и «висящую» в пространстве объемную решетку типа кристаллической.
Полагают, что к числу пространственных диссипативных структур принадлежат также рукава спиральных галактик и кольца Сатурна и больших планет Солнечной системы. На ранних стадиях формирования солнечной системы из таких рукавов исходного газо-пылевого облака сконденсировались планеты, в том числе Земля.
Для высокоорганизованных биологических систем типичный пример временной диссипативной структуры является биение сердца.
Образование диссипативных структур в последние годы многократно наблюдалось и в химиии (осциллирующие реакции), особенно в катализе при исследовании катализаторов методами insitu, позволяющими наблюдать за катализаторами непосредственно в ходе реакции.

49. Временные диссипативные структуры.

53. ОСОБЕННОСТИ РЕАКЦИИ БЕЛОУСОВА-ЖАБОТИНСКОГО.

Реакция Белоусова-Жаботинского – класс химических реакций, протекающих в колебательном режиме, при котором некоторые параметры реакции (цвет, концентрация компонентов, температура и др.) изменяются периодически, образуя сложную пространственно-временную структуру реакционной среды.

В настоящее время под этим названием объединяется целый класс родственных химических систем, близких по механизму, но различающихся используемыми катализаторами (Ce³⁺, Mn²⁺ и комплексы Fe²⁺, Ru²⁺), органическими восстановителями (малоновая кислота, броммалоновая кислота, лимонная кислота, яблочная кислота и др.) и окислителями (броматы, иодаты и др.).

Эта реакция была открыта Белоусовым в 1951г. как гомогенная осциллирующая во времени реакция окисления лимонной кислоты смесью бромата калия в присутствии сульфата церия как катализатора окислительно-восстановительных процессов. В растворенной смеси этих веществ в разбавленной серной кислоте происходят периодическая реакция синхронного восстановления ионов церия, сопровождающаяся одновременным образованием ионов Br^-:

(1)

и реакция синхронного окисления, замыкающая цикл превращений этого иона-катализатора.

(2)

Реакция (2) – автокаталитическая, в ней катализаторами являются продукты реакции, которые и ускоряют протекание самой реакции. Свободный ион Br^-, полученный в реакции (1), действует как сильный ингибитор реакции (2). Поэтому вначале протекает только реакция (1) – до тех пор, пока все ионы Се⁴⁺ не превратятся в Се³⁺. Затем начинается реакция (2), все ионы Се³⁺ превращаются в Се⁴⁺, и процесс начинается сначала. В результате система переходит в состояние, для которого характерно периодическое изменение окраски раствора от бесцветной (избыток Се³⁺) к желтой (избыток Се⁴⁺) и обратно. Колебания продолжаются до тех пор, пока не израсходованы все основные реагенты – органическое соединение и бромат-анион, т.е. пока система находится вдали от термодинамического равновесия и существует движущая сила для протекания общего сопряженного процесса.

Упрощенная схема реакции Белоусова-Жаботинского:

В этой схеме выделяют следующие стадии:

1. Автоускорение, помеченное на схеме знаком (+) и сопряженное с окислением ионов катализатора М^п+:

2. Ингибирование, помеченное на схеме знаком (-):

3. Бромирование восстановителя:

4. Восстановление окисленной формы катализатора и образование ингибитора:

Очевидно, что химические превращения ионов катализатор сопрягаются с основной реакцией окисления бромноватой кислоты. Поэтому в силу вступают неустойчивости стадии автоускорения 1 при некоторых соотношениях между концентрациями реагентов даже в исходно гомогенной системе могут возникать осцилляции концентраций различных по степеням окисления форм катализатора, что в связи с их различной окраской легко детектируется визуально.

Наблюдаемые осцилляции концентраций различных форм катализатора в реакции Белоусова-Жаботинского являются примеров временных диссипативных структур.