Устойчивость САР

На вход системы подается гармонический сигнал, на выходе получается гармонический сигнал с измененной амплитудой и сдвигом по фазе. Так как система линейна, то частота не изменяется

САР называется устойчивой, если, будучи выведенной из состояния равновесия, либо под воздействием извне, она вернется в прежнее состояние после прекращения воздействия.

Для устойчивости системы все корни ее характеристического уравнения должны либо быть действительными отрицательными, либо комплексными с отрицательной действительной частью.

САР находится на границе устойчивости, если есть хотя бы один нулевой корень или чисто мнимый корень, все остальные корни должны отвечать требованию устойчивости(см. выше)

Корень характеристического уравнения в общем случае:

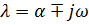
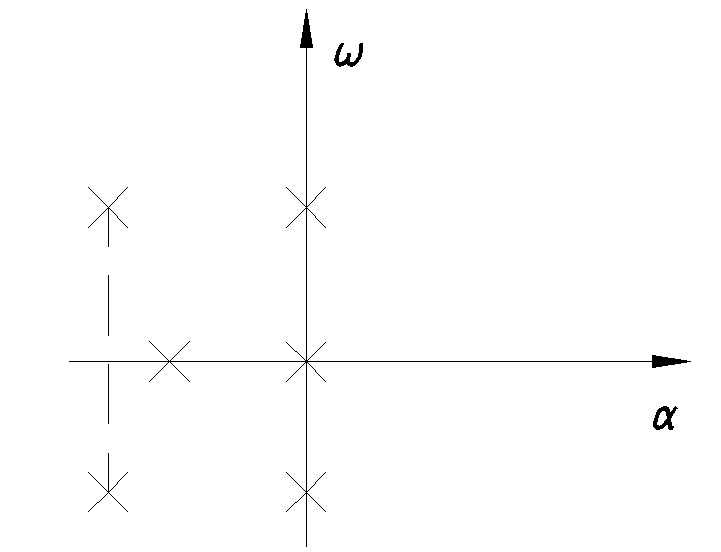
Рис.9.1

Корни характеристического уравнения на комплексной плоскости

Если система устойчива, то все корни ее характеристического уравнения находятся в левой полуплоскости.

Границы устойчивости:

-Апериодическая граница устойчивости: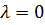

-Колебательная граница устойчивости: корни характеристического уравнения чисто мнимые.

-Граница с бесконечно удаленным корнем.

Общее определение устойчивости

Теория об устойчивости была сформирована Ляпуновым.

Уравнение динамики нелинейной системы в форме Коши:

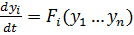, где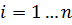

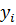- определяет общее движение системы

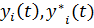-невозмущенное движение системы (установившийся режим)

Введем разность 2 сигналов:

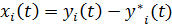-отклонение возмущенного движения (см. Рис.9.3)

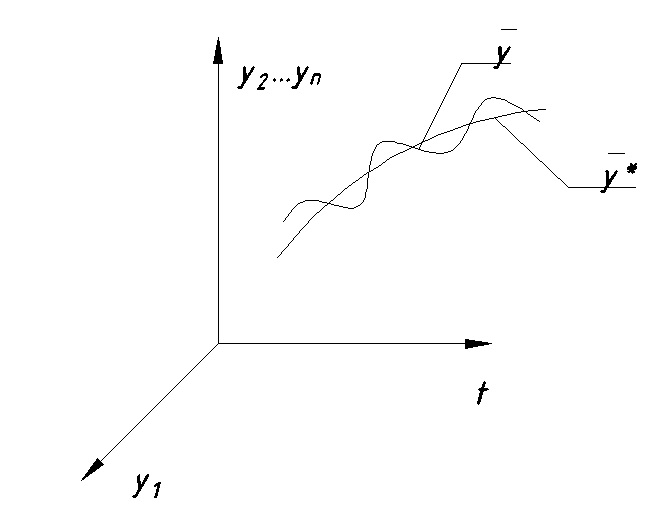
Рис. 9.2

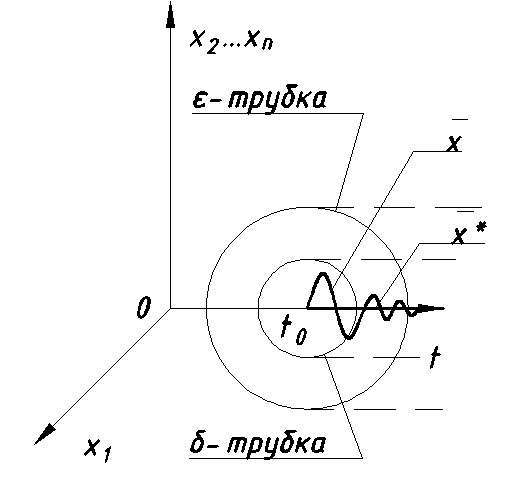
рис. 9.3 Отклонение по ошибке

Примечание: δ-дельта трубка (внутренняя трубка), ε-эпсилон трубка (внешняя трубка)-соответствует допустимым отклонениям.

Аналитическое определение понятия точности по Ляпунову

Невозмущенное движение называется устойчивым, если при сколь угодно малом 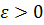существует такая область 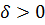, что при всех значениях времени (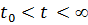),будет выполняться условие 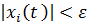, при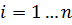

Возможны два случая:

· Случай 1. Асимптотическая устойчивость: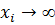

· Случай 2. Система устойчива в целом (в большом): выполняются те же условия при больших начальных отклонениях.

Если разложить нелинейное уравнение динамики в ряд Тейлора, тогда получаем уравнение в отклонениях:

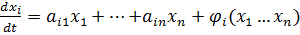, где:

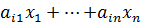-линейная часть

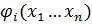-малые нелинейности, которые имеют члены разложения высшего порядка, начиная со второго. После проведенной линеаризации получается приближение:

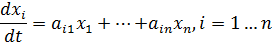
Теорема об устойчивости для линеаризованных систем

1.Если все корни характеристического уравнения линеаризованной части находятся в левой полуплоскости, то система является устойчивой независимо от малых нелинейностей :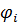

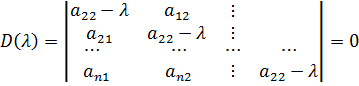
-характеристическое уравнение

2.Если хотя бы один корень характеристического уравнения линеаризованной части находится в правой полуплоскости, то система будет неустойчива независимо от малых нелинейностей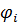

3.Если имеется хотя бы один нулевой или чисто мнимый корень характеристического уравнения, то необходимо учитывать малую нелинейность .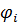

Примечание. На практике пытаются избежать последнего случая и не приближаться к границе устойчивости.

Для исследования устойчивости системы используется много критериев, но на практике широко применяются 3 критерия:

1. Алгебраический критерий (критерий Гурвица)

2. Частотный критерий Михайлова

3. Частотный критерий Найквиста