2015-07-02
200
Покажем сначала, что формула имеет смысл, т.е.что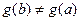 
. (От противного). Пусть 
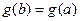, тогда, по теореме Ролля, 
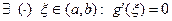, что противоречит третьему условию: 
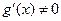для всех х из 
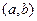. Следовательно, .
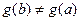Для доказательства введем в рассмотрение на отрезке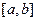 
следующую вспомогательную функцию: 
.
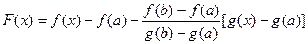1) F (x) непрерывна на отрезке 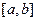, как разность двух непрерывных функций f (x) и 
;
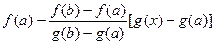2) F (x) дифференцируема на интервале :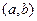 
;
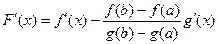3) F (а) = F (b), так как
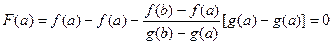и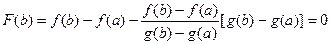 
.
Следовательно, из 1) – 3) следует, что функция F (x) удовлетворяет всем трем условиям теоремы Ролля, тогда, по теореме Ролля,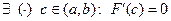 
, т.е.
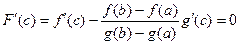, отсюда 
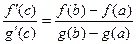. Что и требовалось доказать.
