Доказательство

Так как по условию функция y = f (x) непрерывна на отрезке 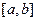, то по второй теореме Вейерштрасса она достигает на этом отрезке своего максимального и минимального значений, т.е. существуют точки 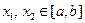такие, что , .

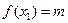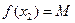Могут представиться два случая:

1) M = m, тогда 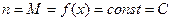. Найдем производную: в любой точке .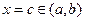

2) M < m, при этом по условию 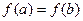, тогда хотя бы одно из двух значений m или M не принимается на концах отрезка 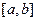. То есть существует точка 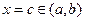такая, что f (c) – наименьшее или наибольшее значение функции на интервале 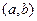. Так как по условию функция y = f (x) дифференцируема на интервале 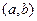, т.е. и в точке х = с, то по теореме Ферма 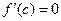, что и требовалось доказать.