Тригонометрия.
I. Тригонометрические функции.
А9. Укажите наибольшее значение функции у = 1 – cos3х. 1) 1; 2) 2; 3) 0; 4) 4.
А9. Найдите наибольшее значение функции у = 2 cosх – 11. 1) -9 2) 2 3) -11 4) – 13
А9. Найдите область значений функции у = 7 + cos x. 1) [-1;1], 2) [-7;7], 3)[0;7], 4) [6; 8].
А9. Найдите область значений функции f(х) = -5 cos x. 1) [-1;1], 2) [1;5], 3)[-5;1], 4) [-5; 5].
А9. Найдите область значений функции g(х) = 2sin x – 1. 1) [-2;0], 2) [-2;1], 3)[-3;1], 4) [-2; 2].
А9. Найдите область значений функции у = 4 cos 2 x. 1) [-4;4], 2) [-8;8], 3)[-5;-3], 4) [3;5].
А9. Найдите область значений функции у = 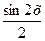 . 1) [-1;1], 2) [-2;2], 3)[-0,5;1,5], 4) [-0,5; 0,5].
. 1) [-1;1], 2) [-2;2], 3)[-0,5;1,5], 4) [-0,5; 0,5].
А9. Найдите область значений функции у = -0,2sin5 x. 1) [-0,2;0,2], 2) [-1;1], 3)[-5;5], 4) [-1,2; 0,8].
А9. Найдите область значений функции h(х) = 3 + tg x. 1) [3;+∞), 2) (-∞;+∞), 3)(-∞;3], 4) [2; 4].
В9. Найдите наибольшее целое значение функции у = 25 ∙ 3cos4x cos3x + sin4x sin3x – 2.
В9. Найдите наименьшее целое значение функции у = 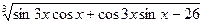 .
.
В9. Найдите наибольшее значение функции у = 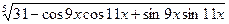 .
.
I I. Тригонометрические уравнения.
А5. Решите уравнение sin3х = 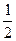 .
.
1) (-1) п ∙ 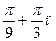 , п Є Z 2) (-1) п ∙
, п Є Z 2) (-1) п ∙ 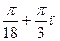 , п Є Z 3) ±
, п Є Z 3) ± 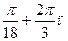 , п Є Z 4) ±
, п Є Z 4) ± 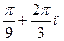 , п Є Z
, п Є Z
А5. Решите уравнение cos2x = - 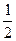 .
.
1) (-1) п ∙ 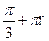 , п € Z 2) ±
, п € Z 2) ± 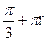 , п € Z 3)
, п € Z 3) 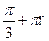 , п € Z 4) ±
, п € Z 4) ± 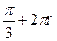 , п € Z
, п € Z
А5. Решите уравнение cos 2х = -1
1) 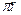 , п € Z 2)
, п € Z 2) 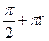 , п € Z 3)
, п € Z 3) 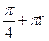 , п € Z 4) -
, п € Z 4) - 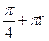 , п € Z
, п € Z
А5. Решите уравнение sin 2x = 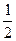 .
.
1) (-1)n∙ 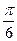 +
+ 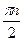 , n Є Z. 2) (-1)n∙
, n Є Z. 2) (-1)n∙ 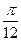 +
+  , n Є Z. 3) (-1)n∙
, n Є Z. 3) (-1)n∙ 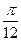 +
+ 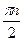 , n Є Z. 4) ±
, n Є Z. 4) ± 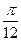 +
+ 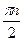 , n Є Z.
, n Є Z.
А6. Решите уравнение 2sinx∙cosx = 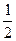 .
.
1) ± 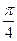 +
+  , n Є Z. 2) (-1)n∙
, n Є Z. 2) (-1)n∙ 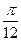 +
+ 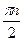 , n Є Z. 3) (-1)n∙
, n Є Z. 3) (-1)n∙ 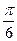 +
+  , n Є Z. 4) ±
, n Є Z. 4) ± 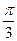 + 2
+ 2  , n Є Z.
, n Є Z.
А6. Решите уравнение 2cosx – sin2x = 0.
1) ± 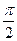 + 2
+ 2  , n Є Z. 2) 2
, n Є Z. 2) 2  , n Є Z. 3) ±
, n Є Z. 3) ± 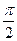 +
+ 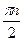 , n Є Z. 4)
, n Є Z. 4) 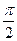 +
+  , n Є Z.
, n Є Z.
А6. Решите уравнение 4sinx + sin2x = 0. 1) корней нет 2) 2  , n Є Z. 3)
, n Є Z. 3)  , n Є Z. 4)
, n Є Z. 4) 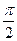 +
+  , n Є Z.
, n Є Z.
А6. Решите уравнение cos2x – sin2x = 0,5.
1) ± 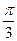 + 2
+ 2  , n Є Z. 2) ±
, n Є Z. 2) ± 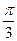 + 2
+ 2  , n Є Z. 3) ±
, n Є Z. 3) ± 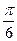 +
+  , n Є Z.. 4) ±
, n Є Z.. 4) ± 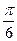 + 2
+ 2  , n Є Z.
, n Є Z.
А6. Решите уравнение 2 sin 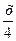 cos
cos 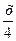 – 1 = 0.
– 1 = 0.
1) π, п € Z. 2) π + 2  , n Є Z. 3) π + 4πn, n Є Z. 4) π + πn, n Є Z.
, n Є Z. 3) π + 4πn, n Є Z. 4) π + πn, n Є Z.
А6. Решите уравнение cos2x – sin2x = - 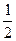 .
.
1)  , n Є Z. 2)
, n Є Z. 2) 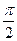 + 2
+ 2  , n Є Z. 3) ±
, n Є Z. 3) ± 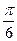 + 2
+ 2  , n Є Z.. 4) ±
, n Є Z.. 4) ± 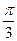 +
+  , n Є Z.
, n Є Z.
А6. Решите уравнение cos2x – sin2x = 1.
1)  , n Є Z. 2)
, n Є Z. 2) 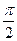 +
+  , n Є Z. 3)
, n Є Z. 3) 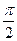 + 2
+ 2  , n Є Z.. 4)
, n Є Z.. 4) 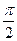 +
+ 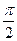 п, n Є Z.
п, n Є Z.
А7. Решите уравнение sin 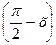 = - 0,5.
= - 0,5.
1) ± 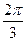 +2πn, n
+2πn, n  Z. 2) ±
Z. 2) ± 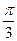 +2πn, n
+2πn, n  Z. 3) (-1) n+1
Z. 3) (-1) n+1 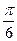 +πn, n
+πn, n  Z. 4) (-1) n
Z. 4) (-1) n 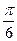 +πn, n
+πn, n  Z.
Z.
А7. Решите уравнение sin(π – x) – cos(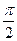 + x) =
+ x) = 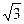
1) (-1)n∙ 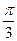 +
+  , n Є Z. 2) (-1)n∙
, n Є Z. 2) (-1)n∙ 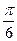 +
+  , n Є Z. 3) ±
, n Є Z. 3) ± 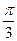 + 2πn, n Є Z. 4) ±
+ 2πn, n Є Z. 4) ± 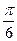 + 2πn, n Є Z.
+ 2πn, n Є Z.
А7. Решите уравнение cos(π+ x) = sin 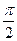
1) ± 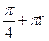 , п € Z. 2) 2
, п € Z. 2) 2  , n Є Z. 3) π + 2πn, n Є Z. 4)
, n Є Z. 3) π + 2πn, n Є Z. 4) 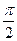 + πn, n Є Z.
+ πn, n Є Z.
А7. Решите уравнение sin х - 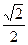 = 0
= 0
1) 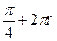 , п € Z 2)
, п € Z 2) 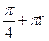 , п € Z 3)
, п € Z 3) 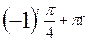 , п € Z 4) ±
, п € Z 4) ± 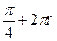 , п € Z
, п € Z
В2. Найдите сумму корней уравнение cos2х – 2 cosx = 3 на промежутке (-5π; 8π).
В2. Найдите сумму корней уравнения 3sin x - sin 2x = 0 на промежутке (-5π; 3π).
В2. Найдите сумму большего и меньшего корней уравнения 2sinx + tgx∙ctgx = 0 на промежутке (-π; π).
В2. Решите уравнение sin2х – 2 cosx + 2 = 0 и укажите число его корней принадлежащих интервалу [-4π; 4π].
В2. Найдите число корней уравнения tg2x + 3 = 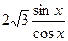 на [-π;
на [-π; 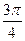 ].
].
В3. Решите уравнение 3sin2x – 2sinx cosx + 3cos2x = 2. В ответе укажите положительный корень уравнения принадлежащий III четверти (в градусах?).
В3.Решите уравнение 7sin2x = 2sinx cosx - 3cos2x + 4. В ответе укажите положительный корень уравнения принадлежащий I четверти в градусах.
В3.Решите уравнение 5sin2x – 2sinx cosx + cos2x = 4. В ответе укажите положительный корень уравнения принадлежащий IV четверти в градусах.
В3. Укажите наименьший положительный корень уравнения в градусах sin(35° + х) = 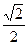 .
.
В3. Укажите наименьший положительный корень уравнения в градусах tg(3х + 45°) = 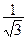 .
.
С2. С2.Решите уравнение 4cos x ctg x + 4ctg x + sin x = 0.
С2. Решите уравнение sin2x + 1 = sin2x + 6ctgx.
C2. Решите уравнение 7tgx + cos2x + 3sin2x = 1
C2. Решите уравнение 2sin2x + cos2x = 1 + 9tgx
 2015-07-04
2015-07-04 2042
2042